Recently I was debating methods for assessing risk-matching among comparison groups with Yale Epidemiologist Harvey Risch in an email. Risch is a brilliant epidemiologist whose dissertation focused on mathematical modeling in epidemiology. During the pandemic, Risch and I have held virtually identical views of efficacy of early treatment medicine, right down to our shared opinion that the evidence in favor of hydroxychloroquine (HCQ) usage is more robust than that of ivermectin (IVM). This is not to say IVM might not turn out to be the better medication, and the documentation for both has been roundly sabotaged, but HCQ simply has a more robust presence in the published literature to date---perhaps partially because a large portion of infectious disease researchers expected for HCQ to be the best chance and set up trials for it early on during the pandemic. It was sad and shocking to see some of his colleagues mount an ugly public attack on him that involved using “The Science” as a cudgel, rather than any real assessment of evidence (and I’m happy to debate the point with any of them).
The disagreement that Risch and I had is over nontraditional methodology I have in mind that would challenge the way risk-matching (prospective matching vs. propensity score matching vs. retrospective observational pools, etc.) gets viewed. He would rather stick to traditional methods with deep literature and acceptance, whereas I believe I have a first principles model that gets to the precise reason why observational results catch up in “statistical power” to match RCT results over time (and it’s not the one usually quoted), though the real problem and solution framing is less simple than that statement. Unfortunately, due to the pandemic, time is precious for everyone, and the discussion we should have should take place over days or weeks when the world is not in crisis. But to be brief, I believe that minimal risk-distance matching (point-to-point matching of scattered individuals along distributions that are more or less easy to guess, thanks to the Central Limit Theorem’s broad applicability to biological systems) can be proved to exist (or else amply demonstrated by Monte Carlo analysis) among populations of sufficient size and ratio. If I’m right, this new observation would challenge the need for economically optimal use of a large portion of RCTs. It would also allow for an enormous amount of new research of cheap and easily produced natural medicines that have not received the attention of more profitable pharmacological solutions.
Though the debate really doesn’t have time to take place at the moment, the thoughts that led to the conversation spurred me to examine a lot of trial literature in a different way during the pandemic. In particular, I’ve started to examine vaccine trials on the level of expressed point attributes. Dropping the mathematical jargon down a bit, I’ve started to ask questions about the properties of individuals in trials by listing their full set of attributes as they relate to the outcomes. I’ll try to make that more clear by the end of this article, including why it matters.
Person-Days as a Measured Unit
One thing that many studies do in order to normalize measurements among populations that change states is to count the number of days each individual spends in each state (such as the state of being vaccinated or the state of being unvaccinated), which we call “person-days” (or more generally “person-time”). Once you get the idea, the reason for it is obvious. If one cohort gets followed for three years while another of equal size gets followed for just one year, we should expect the first cohort to experience three times as many of most forms of events, whether those events are car accidents, headaches, or birthdays. To properly compare associations between events and properties of the cohorts, we normalize event rates by dividing each cohort’s event tally by the measured person-time for each cohort.
The Haas study on the Pfizer vaccine performed such a normalization, as should be expected. That study found high efficacy rates at levels around 94% to 97%, though Dr. Rollergator explained why those numbers can be misleading if you expect for them to be consistent between endpoints (as in Bayesian/conditional statistics). But Haas failed to normalize for another key ingredient to the results (or succeeded in disguising it).
Risk Adjusted Person-Days
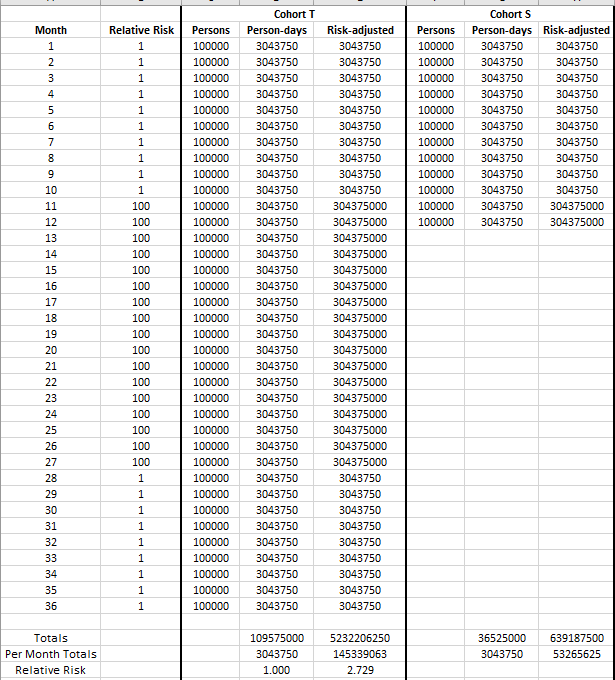
Consider once again the cohorts from earlier. Imagine that we studied them to find out whether height was associated with dying due to gunshot wounds, and we divided them into a taller-than-average cohort (henceforth “Cohort T”) and a short-than-average cohort (“Cohort S”). Imagine that we studied Cohort T for three years and Cohort S for just one year, starting at the same time, but the home nation for these cohorts spent months 11 through 27 in a brutal war funded by the Pentagon for no obvious reason since we cannot fathom that the point of war is often simply profit and dollar dominance.
I digress.
Suppose now that there is no true difference in rates of death by gunshot wounds between the cohorts, but that risk of death by gunshot wound skyrockets to 100-fold the risk of death by gunshot wound during peacetime. The result of the study (assuming sufficiently sized cohorts relative to attrition in person-days throughout the study) would appear to indicate the absurd notion that taller people are nearly 273% times as likely to die of gunshot wounds as are short people.
But we’re rational people, and we don’t really believe that, right?
Forgive my lack of measurement of attrition of the cohort sizes below. I could show it, but I’d just need to correct for that too before final computations.
That study that concludes that taller people die much more often from gunshot wounds...is a dumb study if our goal is to find out whether being shorter is effective at preventing death by gunshot wounds. So, let’s correct it.
The way to correct the study is to multiply each person day by the risk factor of the endpoint that we’re measuring. That creates the numbers in the “risk-adjusted” columns above. Without that correction factor, we make two cohorts of essentially identical risk (well, maybe taller people have a slightly harder time ducking for cover?) look as though they have vastly different outcomes.
Applied to Haas et al
The Haas study examined the time period from January 24 to April 3, a time of declining COVID-19 risk in Israel. This means that more people were passing days vaccinated during the later low-risk period than the high-risk period, while more people were passing days unvaccinated during the high-risk period than the low-risk period. To measure the effect, I took the Our World in Data dataset and performed the calculations above, defining risk as the smoothed 7-day moving average of new cases five days ahead. The reverse lag is an attempt at a mild adjustment at gauging moment-infectivity that is intuitively superior to daily new cases. The result is that, the unvaccinated person-days were scaled by a 1.90 risk factor. Thus a saline solution with no efficacy at all would still result in 45.2% efficacy across the board for all endpoints.
There are more and less perfect ways to properly adjust for the 1.90 risk factor, but the basic results (I’ll skip over the computational details) are as follows:
96% efficacy becomes 92.4% efficacy
95% efficacy becomes 90.5% efficacy
94% efficacy becomes 88.6% efficacy
So, understand that I’m not here to claim a lack of basic efficacy of the Pfizer vaccine in preventing mild symptomatic COVID-19. Training a person’s B cells into emitting a flood of antibodies does that job to some measurable extent. But it is extremely important to point out one of the several ways in which data is being manipulated during the pandemic. It is astonishing that I haven’t seen a statistician lay out this point, and I’m irritated with myself for not having focused on this paper sooner at a point-attribute level.
Note that my newly-adjusted calculations are already eeking closer to my efficacy calculations from the UK’s PHE data for the delta variant, which is to say that delta variant may not have shrunk efficacy by as much as many people assumed. But we are still not done adjusting the numbers! There is still the survivor bias associated with completely ignoring vaccine-associated mortality, which affects the efficacy of more severe endpoints (mortality in particular), and the risk-benefit analysis in particular. I plan to discuss that adjustment in a future article.
These adjustments also fail to account for potential non-observance of an increasing pool of silent COVID cases among the vaccinated who might be infected, but never seek testing due to the lack of symptomatic expression.
There is also the potential for systemic risk-adjustment, which none of the vaccine study authors seem to be examining at all. That would include the introduction of over-confident silent COVID spreaders. That is quite concerning, and I’m still looking for the right words to walk through that topic. Where are the adult statisticians in the room, anyhow?
Conflicts of Interest
I report no conflicts of interest. This study was fueled by coffee and curiosity.
On the other hand...well...I’ll just leave this here.






Brilliant as always! 👍🏽
This is gold. Really first rate.