Bottom Line Up Front: There is no Simpson’s paradoxing around a PRR safety signal. If a safety signal is triggered for the aggregate population, it must be triggered by at least one subpopulation.
A little while ago Steve Kirsch called me and wanted to know if PRR analysis could suffer from a Simpson's paradox. I immediately answered yes and said I could produce an example quickly. I turned out to be wrong, which took me some playing around to realize. I was able to generate signals in the aggregate that were not present in one or another subgroup:
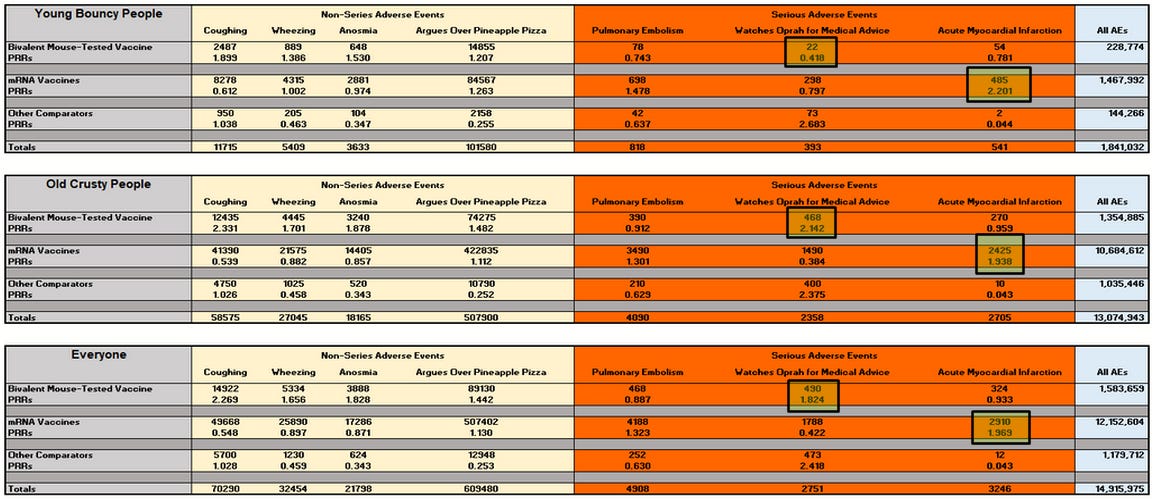
For the Bivalent Mouse-Tested Vaccine, there is no safety signal in the aggregate for the SAE of Watching Oprah for Medical Advice, though there is among the elderly. Similarly, there is no safety signal in the aggregate for Acute Myocardial Infarction, though there is among the young. Thus, the aggregate population can fail to yield a safety signal that would be present in one of the subgroup demographics.
Steve was just writing about these topics here:
I thought I might also be able to produce safety signals in all the subgroups for some AE without it showing up in the aggregate. But as I began manipulating numbers, I started to suspect that I was wrong. And then I proved that it is impossible to trigger a PRR safety signal for some AE in the aggregate without it existing in at least one subgroup. I think the easiest one uses Jensen's Inequality. For each AE, the PRR for the aggregate is bounded by the minimum and maximum PRRs among the demographics. Thus, if the PRR for the aggregate shows a signal, so too must the PRR for the demographic with the maximum PRR among all demographics. Since we can treat c and d as dependents of a and b, we can simplify a proof. For t = 1/2,
Reminder of the definition of the PRR:




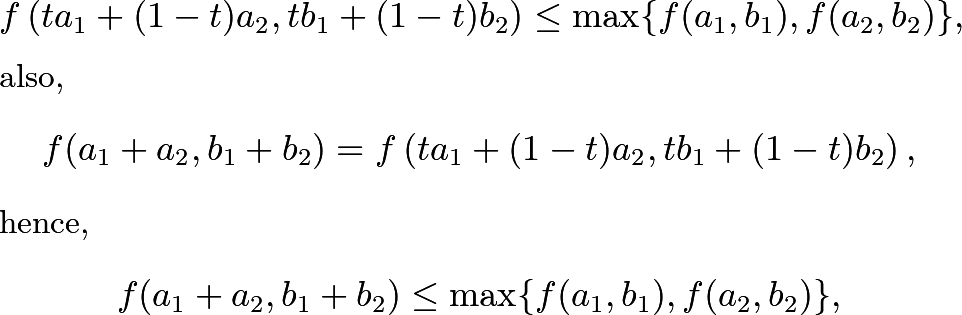

Apologies for the several edits. My first writing was lazy.
Maybe this is not a math problem?
Maybe it is a psychopath problem?