How to Rig Research by Statistically Stacking the Deck (A Simpson's Paradox Tale)

The Chloroquine Wars Part IX

“The generation of random numbers is too important to be left to chance.” –Robert Covey

Suppose that we want to rig a medical study despite the participation of mostly or entirely caring doctors and researchers with unimpeachable character and credentials. We wouldn't want anyone to suspect a thing. We would want for all those involved to be proud of their participation in the name of medicine so that any problems detected could be kept in their mental periphery, dismissed into nothingness by the force of cognitive dissonance. We would want for them to voluntarily speak out or write to dismiss critiques of the research as the conspiracy theories of nutjobs.

You might think the task impossible, or its successful execution improbable. Unfortunately, you would be wrong. Engineering false or misleading research is quite simple once you understand the statistical recipe.

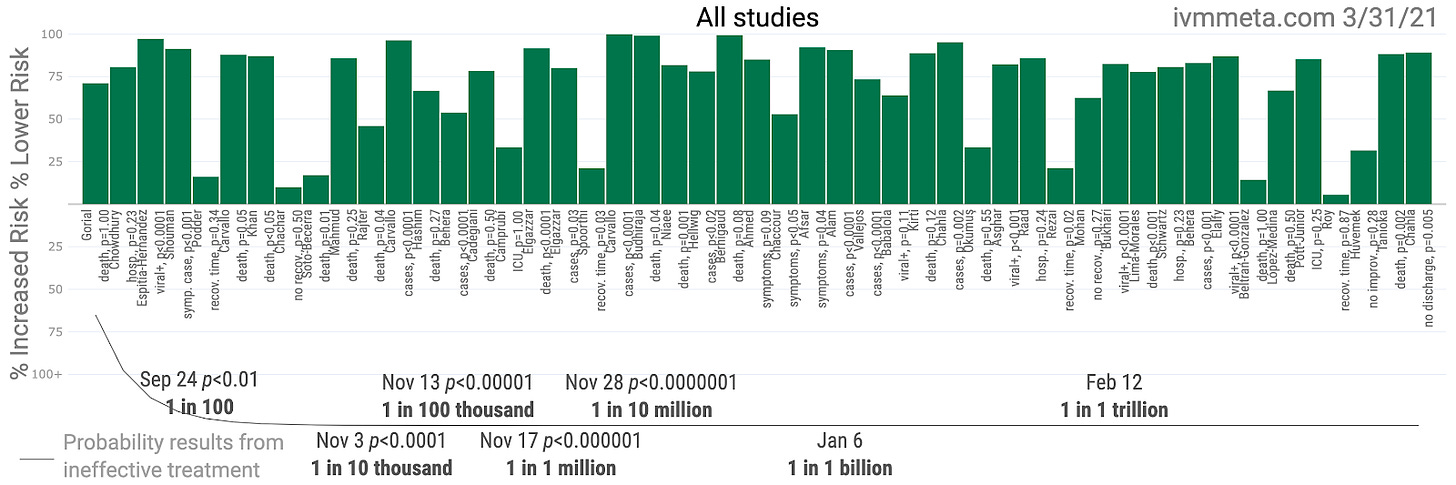
Now, there may be cruder ways to go about rigging research than staging a grand illusion. We might fool people (attending physicians included) by throwing already-medicated patients into the control group of a trial. In one experiment, Brazilian researchers who categorized medicated patients as part of a control group during a hydroxychloroquine (HCQ) RCT still got published in the prestigious NEJM, and their work is often cited (here, here, here, and here, not to mention in over 250 published research papers to date) as part of the definitive case against HCQ (despite the basic illogic of the conclusion with respect to the Primary HCQ Hypothesis that early treatment shows clear success).

We might also fool everyone by swapping pills for at least some of the patients in an otherwise underpowered experiment. After all, there is an inherent Byzantine Generals' Problem in knowing who received the medicine being tested and who received a placebo in a double-blinded randomized control trial. While I'd love to say, "that sort of scheme probably wouldn't succeed," that all comes down to who broadcasts the results and how much time people spend verifying the details. 

In a recent paper on a trial conducted in Colombia, published in esteemed JAMA, a pharmacist did notice that the drug tested on COVID-19 patients (ivermectin) was sent to patients in the control group. While it is unknown whether or not all of the remaining patients left in the final calculations for the control group were medicated with ivermectin or not, the result (in which patients in the treatment arm outperformed those in the control arm, the latter of which performed unexpectedly well, to a degree that did not reach statistical significance) was paraded all over the internet obscuring the tremendously successful track record of ivermectin studies to date (p < .000000000001).

Leaving behind these methods that risk discovery (which might or might not discredit our case, apparently), we can still successfully rig research so well that nearly all experienced doctors, professors, researchers, and even many professional mathematicians would never imagine the fraud if they did not witness the crafting of the illusion with their own eyes. The most clever statistical magicians have a lot of tools in the tool box to work with, if they are creatively inclined. Under the right conditions, all it takes to stack the deck so as to guarantee a credible-looking, but highly misleading outcome is to shuffle together the data from different hospitals with different treatment philosophies for use of the same medication within the same study. 

That's it. That's all. You might be surprised at how radically we can engineer misleading outcomes, or how easily misleading outcomes can be generated by those who do not understand statistics deeply. Let us now walk through a hypothetical example in order to demonstrate the point...

For the purpose of demonstrating the proof of our concept, let us imagine a fictitious medicine called antidumbvirus, or ADV, that successfully treats those infected with SARS-CoV-2. We endow ADV with antiviral properties, plus some other benefits in limiting the damage caused by the inflammation and thrombosis associated with COVID-19. Assuming the existence of ADV, the best protocol for treatment is the moment symptoms begin. 

Now, let us assume that ADV is so extremely effective that,

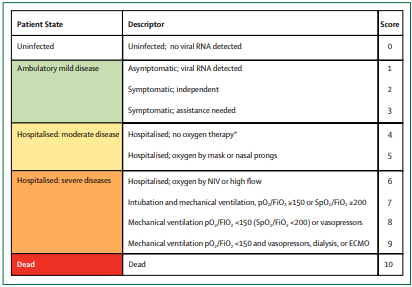
• The mortality rate of those who begin a regimen of ADV within the first five days (generally stages 1 or 2 of COVID-19 as per the standard ordinary scale below) of symptoms is an extraordinary 99% lower than those who receive no medication.

• The mortality rate of those who begin a regimen of ADV at the point of Stage 4 illness (as per below) is 60% lower than those who do not.

• There may or may not be small mortality benefits to those medicated with ADV at illness stages 6 or above.

Source: WHO

Now, consider three types of hospitals categorized according to ADV treatment of admitted COVID-19 patients. There may be a handful of patients with contraindications for whom a doctor might not prescribe ADV, so assume those exceptions are built into the data.

• The first hospital treats (essentially) all patients early, immediately upon hospital admission, with ADV.

• The second hospital only treats patients with ADV if they reach an advanced state of illness: severity score 6 or above. This might be called a "compassionate use" policy. 

• The third type of hospital eschews ADV treatment entirely, providing only the minimal standard of care (SOC).

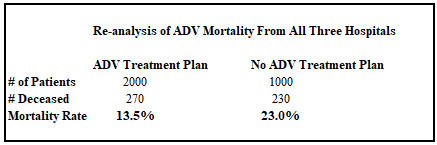
In our hypothetical scenario, each hospital receives 1,000 COVID-19 patients, all at severity score 4 of the COVID-19 disease state (to keep things simple), and fewer of the patients treated with ADV progress to more advanced stages of illness. The hypothetical endpoint result is that patients at Hospital 1 suffer 61% lower mortality (9% vs. 23%) than the untreated patients at Hospital 3. However, when we shuffle together the data from all three hospitals, the retrospective analysis categorizes patients simply as “ADV” or “No ADV”. This results in the bizarre inversion of results as it appears that the patients treated with ADV died more often. 

Some readers may stop and wonder how this could be true. We set up our hypothetical scenario under the assumption that ADV effectively treats patients. How could the final mortality analysis show the untreated patients recovering more often?!

The opposing trends that we see in the data are what is known in statistics as a Simpson’s paradox. This can happen when data gets sampled unevenly across some important variable---in this case that variable is COVID-19 severity [at the time of treatment]. 

Due to the presence of Hospital 2, the 500 patients there who recovered most quickly (who were destined to live no matter what treatment plan they were assigned) were assigned to the “No ADV” category. Meanwhile, ADV treatment only started for those 500 patients most susceptible to the disease after they reached COVID-19 severity score 6, an extreme condition. Then 180 of those patients died, whereas only 90 of those 500 analogous patients died in Hospital 1, and 230 of those analogous patients died in Hospital 3, showing clearly that

Hospital 1's Plan > Hospital 2's Plan > Hospital 3's Plan.

There are many methods used in attempts to fix such flawed analysis as often occurs in retrospective studies. In practice, these methods are fraught with the biases of the researchers and biostatisticians handling the data, and there is no guarantee that they understand how to best employ those methods. In my experience having read thousands of papers, the proportion of misapplications to correct applications is somewhere between 10:1 and 100:1. This makes it highly likely that our scheme succeeds, or is at least defensible in the eyes of most everyone in the industry.

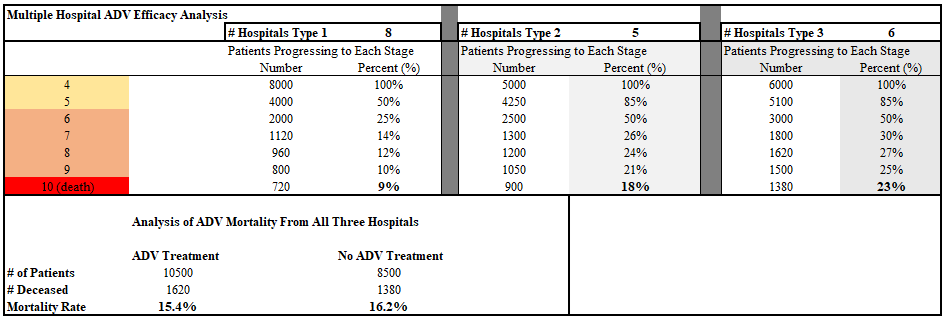
Some methods for correcting data are more useful than others, but none are sufficient without segregating the data entirely by treatment protocol. As we can see in the following table, even attempts at categorizing data by aggregate description such as "used ADV with [some or all] patients" vs. "never used ADV" fails to capture the observed 61% reduction in mortality between the optimal protocol and absence of treatment.

The result of this overly generalized aggregation is that patients at hospitals that use ADV to treat patients have a 41% lower incidence of mortality---which looks good, but not nearly as good as the 61% mortality reduction for patients treated as early in the disease progression as hospitals typically see patients. The end result is that our sabotage of the data is still somewhat effective! In fact, even trained biostatisticians rarely recognize or advocate the observation that the 41% statistic is almost certainly lower than the real effect.

Now, let us imagine the design of an actual research project. Let us contact hospitals in the area and find several with each treatment protocol. We may or may not have to talk some hospitals into adopting the Hospital 2 "compassionate use" protocol in order to ensure as many patient series as possible that use ADV on the most sick patients while leaving those recovering on their own unmedicated. We have influence, and being the clever statistical engineers that we are, we can probably find the right language to persuade some hospitals not using ADV at all to at least try it that way. The result is that the data is harder to tease apart. Let's take a look at a group of 12 such hospitals, with only 3 not using ADV at all.

Now, we can publish our study showing that those who received ADV died 55% more often than those who did not! Not bad for a drug with the potential to save 99% of patients!

Skeptical Take: In reality, it might be hard to steer the numbers. How does the analysis look with other numbers of hospitals?

So long as hospitals of type 2 exist, it takes a tremendous number of hospitals of types 1 and 3 to make ADV look good. In fact, let's double the number of hospitals of types 1 and 3 and see:

Now patients who received ADV died at a rate 5% lower. But that's not statistically significant. Now we just tell the press that "ADV failed to show any benefit in a rigorous study on a large number of COVID-19 patients" and call it a day.

Even better---we can rinse and repeat just a handful of times in such a way that the thousands of patients lumped into this sabotaged analysis stand firm as a rock muddying the collective analysis of essentially all meta-studies [that include any hospitalized patients at all]. And if hospitals of type 2 exist without our meddling, then all the better. We just have to act ignorant about the flawed rubrik of analysis, or make sure the flawed studies take place. That's not hard, and we look heroic for taking action. 

On May 11, 2020, Eli Rosenberg and colleagues published a retrospect analysis of 1438 hospitalized COVID-19 patients in JAMA "showing" that patients who received HCQ or azithromycin among a subset of New York hospitals died more often than those who did not. The results stand out in contrast with the vast majority of retrospective studies from around the world where hospital protocols are typically more uniform. A re-analysis of data from this study by Clinton Ohlers noted that many of the patients from the Rosenberg study were not medicated until they were on death's door. Under the assumption that HCQ does not help such patients, Ohlers showed that moving those patients into the "not medicated column" (which is the best fix available to the aforementioned treatment protocol aggregation problem without access to the individual hospital data) resulted in the demonstration of a clear mortality benefit for those treated earlier with HCQ! If such a correction is inappropriate, that would only be under the assumption that HCQ does benefit the most ill patients. Twitter quickly censored Ohlers and his article from its platform. As Ohlers points out, Rosenberg's faculty profile at the University of Albany states that since March, 2020, 

"Rosenberg has been providing technical assistance to the State of New York's COVID-19 response across a range of activities and studies addressing critical aspects of SARS-CoV-2 transmission, surveillance, prevention, and treatment. He has been providing expertise on COVID-19 epidemiology to Governor Cuomo's office, the SUNY system, the University of Alberta, and in numerous local and national media appearances."

I wonder if he performs at children's birthday parties, too.