Puzzles and Strategy
Appreciating Mathematical Beauty Volume 7
Find other articles on Mathematical Beauty here.
A friend just shared a fun puzzle on Facebook. It's nothing momentous—we aren't squaring the circle or figuring out how to get people to question whether a nonviolent old man out for a walk in his robe could actually chase away an empire that killed hundreds of millions of people. Give it a try.
If you find this puzzle challenging, understand that my friend is a top notch engineer, and he admits to finding it moderately difficult. Of course, difficulty is a matter of what we have trained ourselves to accomplish. I see him talk about engineering projects I would not know how to approach (though I have learned from his posts, which I appreciate). I find this particular puzzle simple because it is in my wheelhouse.
Now, I’ll create a little space between the puzzle and solution using a video of one of my now nine-year-old cats, Nissa, back when she was just a little kitten learning about Platonic solids.
Mathematical Strategy: Organizing Information
One of the reasons people get fooled by information is that it isn't always obvious when the arrangement of information presents a simple problem or a hard one. Some of the most fascinating mathematics, historically speaking, involves seemingly simple problems—or at least simply stated problems—that go unsolved for decades or even centuries. The simplicity of the basic tools of a problem can be deceiving.
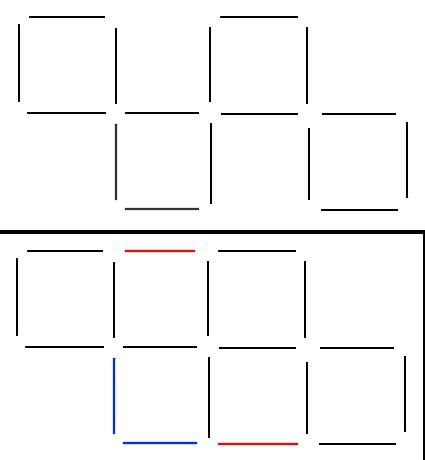
One of the conceptual strategies a good mathematical problem solver learns is to take stock of the combinatorial properties of a diagram. In this case that just means counting the sticks. There are sixteen of them, which is 4 x 4. This tells us that each of the four final squares will share no sides. This means that we need to move two sticks in order that no two neighboring squares are both still squares. A bit of intuition also suggests an alternating pattern, with a final position of two squares on each of the two rows in the diagram (it would take moving at least three sticks to form a square on a row other than the original two).
The solution:
Ooooo, this is a fun one. I’m gonna give it to the twins and see if a child with less knowledge might come up with the answer faster than I would have. Sometimes solutions are prevented by overthinking.
It is indeed easy, once you see it. It was obvious that, since there are three in the upper row, one must be gotten rid of, but I couldn't figure out how. Now it is obvious that to make four squares with sixteen sticks, none can be contiguous.