Flooding the Zone With Lies

Information Wars Part II

"We know they are lying. They know they are lying. They know that they know they are lying. We know that they know that we know they are lying. And still they continue to lie." -Alexander Solzhenitsyn

What's the point, then?

Is every lie a loyalty test in a perpetual game of thrones played mostly by the "fittest" kunlangeta?

Certainly not.

Are so many lies for something noble like "your own good"?

In the eyes of each beholder, the question is isomorphic to "Is Santa Claus real?"

Are some lies simply the web-work of gaslighting sadists?

Yes, but that's its own problem, and only tangential to the far larger body of lies.

Are so many lies for the purpose of controlling profit?

Sort of, but sort of not. In fact, given a sufficient amount of time, assuming there is no limit to technological development, the liars would be wealthier in a world without their lies, whether or not they know it. Sadly, there is no way for them to recognize their mistakes in terms of optimal evolutionarily stable strategy. Or perhaps the kunlangeta simply prefer power to wealth because their defined mental/emotional disorder clouds the basic understanding of the latter without the former.

We could go on asking questions, and perhaps there are many good questions to ask? I'm certain of it. But let's pick a productive path through the maze. In fact, let's talk about the maze.

---

A Basic Information Theory Problem and Solution

The field of information theory covers the quantification of truth and entropy in information transmission. The most commonly discussed applications in the public sphere might be computing applications such as lossless and lossy data compression. But at the underpinnings of information theory lies a very basic statistics problem that explains a key aspect of the lies of large governments.

Consider the following problem: some drone rover plops down on Mars and begins gathering data. That data gets stored as binary numbers which are at some point transmitted back to Earth, possibly through some intermediary or intermediaries. As anyone who has ever talked on a cell phone knows, there is no guarantee that the information is always transmitted perfectly. Either due to interference of energies or imperfections in intermediaries, some of the binary digits get miscommunicated. Is there some way to recover the truth of the information?

The answer is a very statistical and economic 'yes'. First I will explain the basic solution, then why it is a statistical solution only, and then what economics has to do with it.

A parity bit (also parity digit or check bit) is a digit that gets appended to a sequence in order to induce a particular property to the resulting digit string. The goal is nearly always to create a binary string with an even digital sum (an even number of 1's). Examples from the linked article:

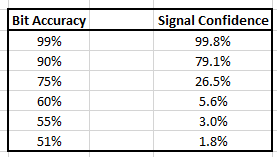
Suppose that a signal is known to be 99% accurate in the transmission of each single bit (binary digit). Then we can compute that each 7-digit binary string has a 93.2% chance of being transmitted with complete accuracy. However, when we add the parity digit, we gain the benefit of a cleverly induced conditional circumstance. When the sum of the digits in the 8-digit string (which includes the parity digit) is even, we compute that the probability that the string of information is fully accurate is 99.8%, which is quite close to 100%. While this does not represent certainty of truth of the received signal, it is a vast statistical improvement in our confidence!

Now we might build in a communication feedback loop to clean the signal, if possible, and recover most or all of the pieces of the transmission that look dirty (have odd digital sums).

Now, consider what happens when the bit accuracy falls from 99%. Our statistical solution degrades in value:

If the bit accuracy rate falls below 50%, like to 40%, we just change all binary digits to get back above 50% to 60%, then perform our statistical "fix". This means that the worst possible bit accuracy rate is 50%, which is to say total randomness. At that point, there is no way to identify problematic strings in the transmission, so no way to clean the signal.

Fortunately, there are further ways to continue to improve our confidence in identifying and cleaning dirty signals, but they come at an economic cost. The task can grow so challenging as to be the subject of doctoral research and whole teams at motivated tech companies. We can add digits at various intervals to induce additional parity properties to improve our confidence in the signal. We can spend on software and hardware and energy to perform more and more checking. Trust, but verify. Check, check, check, check, verify, verify, verify, verify.

But the cost grows and grows and grows...when the lies get harder and harder to distinguish from the truth, and more costly to check. Even worse, those expenses put authoritarian adversaries at an economic advantage, and in any combat, expect those with the economic advantage to win (and thoroughly). The harder the information flood of truths and lies, the larger the maze to reach understanding.

What's the point of all those lies when we know that the lying liars lie so often that there is general recognition of the game of dirtying all the information signals?

It's to put you into the position of making a terrible choice: take the Faustian bargain and try your luck in the authoritarian hierarchy, accept virtual enslavement, spend all of your resources checking the lies in hope that the truth will free you (meaning everyone at once or likely no one), discover a new technological leap that fundamentally changes the game, or commit to revolutionary war.