Are UK's Vaccinated Dying More from the Delta Variant?

The Chloroquine Wars Part XXXVI

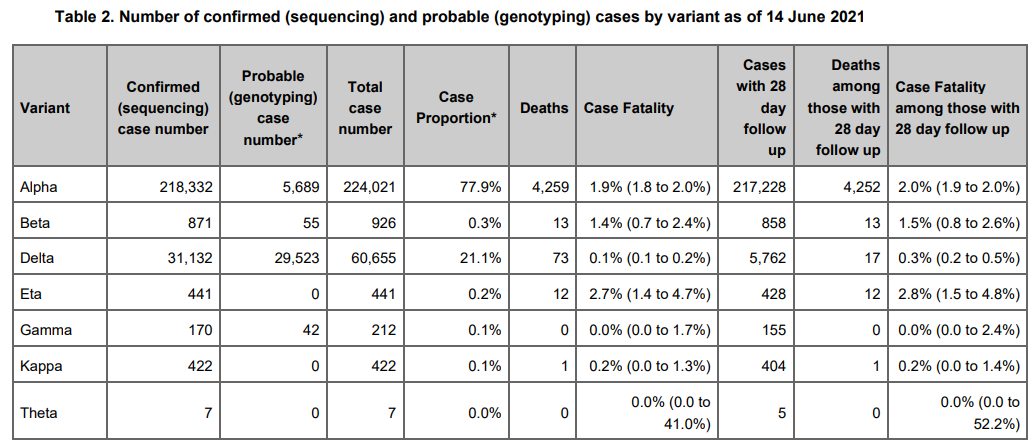
A controversy recently broke out over the data coming out of the Public Health of England (PHE) breaking down cases and fatalities by vaccination status for those COVID-19 patients infected by the SARS-CoV-2 variant known as the B.1.617.2 Delta variant. I decided to take a closer look at the numbers because I've been skeptical of the efficacy numbers claimed by vaccine manufacturers for more reasons than I'd like to write about in this article.

Before I jump into the data related to vaccine efficacy, I'd like to point out some extremely good news. As scary as the Fauci-driven media might make the Delta variant sound, the PHE data shows it to be far less deadly than previous variants! In fact, the case fatality rate (CFR) for this variant may be nearly 94% lower (Edit: after changes of variables as per below, this number looks to be in the 80% to 93% range after proper adjustment, assuming no vaccination). Viruses do usually evolve into less deadly forms in populations they inhabit due to selection for living hosts, but such a large reduction in CFR is surely unexpected. I have not searched for data from other nations to check for consistency, but let us all hope this is the case. It is also worth noting that this would mean that the Delta variant reduces any margin at the risk-benefit level for the vaccines.

On face, the PHE data doesn't look great for the vaccines. There are slightly more deaths among half as many cases among the vaccinated. In fact, per COVID-19 case, there are almost exactly 2.5 times as many deaths among the vaccinated.

However, there are extreme biases between the vaccinated and unvaccinated groups that need to be taken into account to get anything like a reasonable picture of vaccine efficacy and it would make no sense for the Delta variant to show a dramatic increase in death by COVID-19 (assuming only the standard definition) that we would not have noticed in other variants. In particular, the vaccine campaign targeted high risk groups first, so unless the efficacy rates are extraordinarily high, we might expect for there still to be more deaths among the vaccinated group.

I set about running the numbers to get a reasonable answer, or rather a range in which the true answer probably lies. An epidemiologically perfect answer is impossible without raw data, but I think I've found a pretty solid way to examine the problem. Note that the UK has used the Pfizer, Moderna, and Oxford/AstraZeneca vaccines. It is impossible from the PHE data only (or any other information I found) to tease the real world effects of these vaccines apart.

The first thing I wanted to do was to establish something like a risk curve where I could break down each point on the curve into ((0 jabs), (1 jab), (2 jabs)) at which point running the numbers would be a simple exercise. Of course, no such curve exists. The best we can do is look at risk magnification factors, and the first variable I examined is age (data found at gov.uk here).

Note the "<10" entries. This is due to regulations for data reporting that is supposed to de-identify data in a statistical sort of way. But in reality, there is enough information in the chart that I was able to impute those values exactly (forgive the unexplained value artifacts):

No sooner had I set up this portion of my spreadsheet, I realized that the PHE report lacked this kind of risk curve. But this set me thinking:

• Only 2.3% of COVID-19 deaths are under the age of 50 in the UK. I've seen similar numbers, but it always jumps out at me due to the way it affects a risk-benefit analysis (which has still never been performed by the pharmaceutical companies or health agencies).

• Almost 60% of deaths are among the 5% oldest citizens of the UK (those 80 or older).

Perhaps as a good exercise, I can simply define "high/medium/low" risk groups due to the high risk and low risk groups representing such extremes that we might simply view as relatively uniform within each group. Sure, that assumption of uniformity will throw our answer off, but I've already acknowledged the necessity for a reasonably good, but not perfect answer. Further, this is where we can plug in numbers to create a range of outputs.

Variables we have and variables we need:

1. Sizes of risk groups.

2. Proportion of cases and mortality split among the risk groups.

3. Percent of each group that got the jab.

For the first of these, I chose to estimate reasonable sizes of the groups. I rounded the UK population to 65 million and put 5 million in the high risk group. This seemed like a reasonable way to combine most of the 80+ elderly with the most susceptible among all other groups. This is the most important group as it represents the vast majority of all fatalities (the percentage of which becomes a new variable at this point). I threw 10 million into the medium risk bucket, and the remaining 50 million into the low risk bucket.

For Variable 2 above, I eyeballed case curves I've seen showing cases to be far more closely uniform among age groups than are the deaths and decided I could estimate the case breakdown within reasonable limits, regardless of exactly how we defined the risk groups. This should be apparent down below.

Variable 3 is where a lot of the range testing happens. In casual conversation, I saw suggestions that 90% or 100% of the high risk group were vaccinated. I'm not so sure the numbers are that high for several reasons. Consider this report from the UK.

• Vaccination rates fall from 92.6% to 71.1% from the 80-84 age group to the 100+ age group.

• Vaccination rates among the elderly in higher risk races/ethnicities are substantially lower than those of the majority white population. The UK's elderly black population, for instance, is less than 60% vaccinated.

• Vaccination rates are lower among the disabled, and we should assume that the most frail are often considered to be too weak to receive or want to receive the vaccinations (and handle the substantial adverse events).

• Some vaccine contraindications are correlated with more severe outcomes.

• Some among the higher risk are unidentified people with a specific autoimmune condition that sharply increases COVID risks (here and here).

As my personal best guess, I'm using 84% vaccinated among the high risk group, 78% among the medium risk group (using the 59% vaccination rate from June 1, this mix resulted in 53% among the low risk group which does include the very young who are sparsely vaccinated). But as I said, I will present a range of results based on plugging in different values. Here is one example where I've plugged in 85% and 14.5% as assumed (prior) proportions of deaths associated with the high and medium risk groups. Since risk factors stack, and mortality is only on the extreme tail of the distribution, I chose a fairly high proportion of deaths for the high risk group. Click to (hopefully) enlarge:

Here is the input/output section enlarged:

Of course, my formulas are obscured, but I checked assumptions to my level of comfort. The results:

• The relative risk reductions (RRRs) for COVID-19 cases are 34.2% and 86.9% for 1 jab and 2 jabs, respectively.

• The RRRs for COVID-19 mortalities are 76.5% and 74.1% for 1 and 2 jabs, respectively.

This is quite interesting! Part of the controversy over the jabs is that adverse events after the second injection, the adverse events are substantially elevated. Is it worth getting the second jab for a reduction in cases, but not a reduction in mortality? And for whom? If the risks resulting from COVID-19 are so low already for the low risk group (2.3% deaths were for people under 50, and only 8 deaths total below the age of 20), then the absolute risk reduction is necessarily small---perhaps so small that a single dose is a bad idea. If there is no further mortality reduction, and adverse events are substantial, then a second dose might be a truly terrible idea. But, of course, this is the reason why we need a risk-benefit analysis to be published.

Now, let's look at a reasonable range of results after plugging in different variables. Example 2 primarily reduces the proportion of deaths ascribed to mortality (prior to the vaccination campaign) while raising the vaccination rates of the high/medium risk groups:

The vaccines still show protection---at least according to standard definitions, but a bit less than before.

Example 3 configures the variables intentionally to examine something plausible as a worst case scenario for the vaccines.

We see stable case efficacy through these variable changes, but the effect on mortality is substantially smaller. We can already see that defining efficacy as the prevention of mild cases as was the case in the COVID-19 vaccine trial reports does not at all necessarily translate to a similar reduction in mortality. But in this scenario that is in the ballpark of a worst case, the second dose does improve the RRR for mortality.

Example 4 configures the variables intentionally to examine something plausible as a best case scenario for the vaccines.

Under this set of assumptions, the vaccines show an excellent impact on mortality. Of course, we still need a risk-benefit analysis to understand for which parts of the population such a RRR actually translates to "worth the price". I plan to write about that more in a future article.

Finally, example 5 is back to inputs that I consider reasonably within the realm of mostly likely possibilities:

Some notes on these examples:

• It bothers me that the RRR for mortality from 1 jab is so much higher than the RRR for cases.

• Inclusion of the proportions in each group of the previously infected/recovered might alter the conclusions.

• Without an excellent risk curve or the raw data to engineer one, we can fairly estimate the RRR for cases, but not for mortality.

• Under a lot of assumptions, the implied RRR on mortality is better for 1 jab than for 2 jabs. While some may debate about various harms of the vaccines, those are largely separate arguments. The 71 deaths is small enough that this might have resulted from random chance.

In conclusion, I disagree with those who say that the data shows that the vaccines increase mortality [from COVID-19 alone]. It may be that the reduction in deaths does not justify the deaths and serious adverse events caused by the vaccines, or that a complete risk-benefit analysis looks negative, but purely based on the PHE data, the vaccines show some efficacy, though not as much for the Delta variant as was promised by the trial reports.

I'm sure my analysis is incomplete, and so my conclusions may be incorrect. Take this as a two hour long exercise that took longer to write about (maybe three) than to put together. I took the project up to see what I might learn, which is plenty, though I'm left with plenty of important questions. I hope this was a valuable read for many who are curious. If you have any thoughts to add, please leave them in the comments. I'd love to learn more from Rounding the Earth readers. If what I learn changes my perspective on the data completely, perhaps I will perform a second analysis to get closer to the truth.