The Nudge as a Tool for Social Control, Part 1

The Kunlangeta Part XII

"Manipulation is a contagious disease, much more dangerous than the flu because it can endure for a lifetime." -Dorothy Mccoy

In their best-selling book, Nudge: Improving Decisions about Health, Wealth and Happiness, economist and behavioral scientist Richard Thaler and legal scholar Cass Sunstein explain how subtle interventions ("nudges") that influence consumers have large downstream effects on their behavior. The authors argue that seemingly small psychological changes, such as the order in which choices are presented, result in substantially changed behavior. How do small changes spiral into substantially improved outcomes? What should be our takeaway from this observation?

---

Understanding the Nudge

Understanding the nudge does not necessarily require something like full understanding of complex systems. Thaler and Sunstein's primary observation is a clever one because instead of taking on whole systems with dozens, hundreds, or potentially thousands of variables, they focus on the effect of one or a small number of variables at the extremes of distributions. Mathematicians and other problem solvers often refer to their approach as the extremal principle. I will try to make this clear and simple for readers who are not statisticians.

In complex systems in which outputs (results) are influenced by massive numbers of inputs (variables). Take for example the height of a human being. In a 2014 study involving around 250,000 people, over 400 gene regions in human DNA were found to affect height. That’s a lot of inputs! And it’s highly unlikely researchers found them all. But wait, the story isn’t even that simple. Firstly, many effects are not merely genetic, but epigenetic, meaning the outcomes are determined by an interplay between genes and other environmental influences, including stressors (e.g. toxins, traumas, radiation, cable news networks) and health behaviors (e.g. sleep, nutrition, physical activity, watching cable news networks). So, each genetic variable really splits into hundreds or thousands of other variables (or more). As a result, identical twins with identical DNA can grow to heights that differ by several inches (though it may be that case that most of that difference is determined prior to emergence from the womb).

Now, in order to take a first step into this topic, we make a simplifying assumption that we can work with. Though effect sizes of inputs on an output may not be the same, let us imagine for a moment that they are the same and see what we can learn. We'll come back to this assumption later.

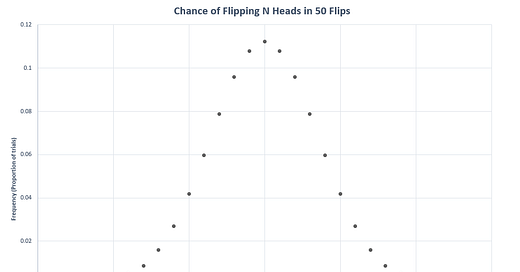
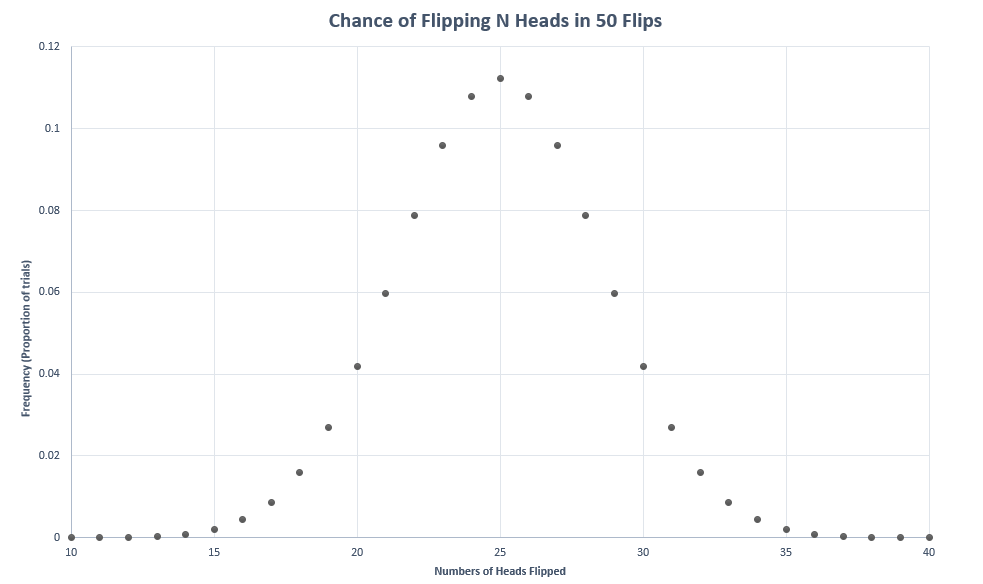
imagine each variable is a coin that gets flipped. If we perform the task of flipping a coin 50 times, we expect to flip heads 25 times. But rarely will we see exactly 25 heads. We might see 18 or 29 or even 50 (though you’re substantially more likely to win the lottery than to see 50 heads in 50 flips). Now suppose we perform the 50 flip task again, and again, and again---trillions and trillions of times. Each time we run such a “trial”, we record the total number of heads out of 50 flips. And when we’re done, we compute the proportion of the number of times that each possible number of heads was recorded, all the way from 0 to 50. The graph will look like this: 

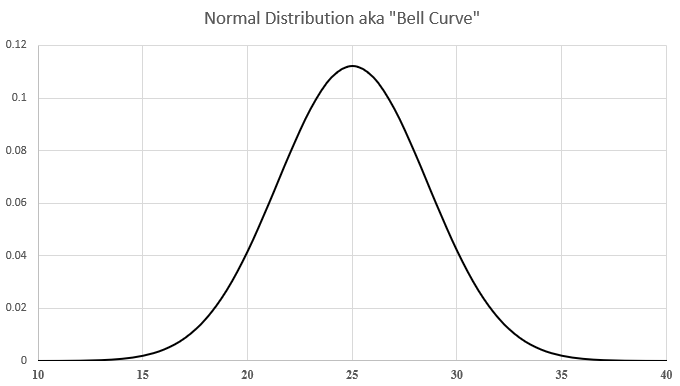
We call the results a binomial distribution (the discrete version). Its close cousin (the continuous version) is the normal distribution, which is the famous bell curve shape. 

These are perhaps the most commonly observed distributions insofar as they approximate natural phenomena. This is because many kinds of natural phenomena are each the result of many inputs (many flips of a coin). For the sake of simplicity, we will refer to both of these distributions as simply “normal” for the remainder of this article. The unfamiliar reader may choose to look them up to find out the slight difference (what “discrete” vs. “continuous” means in statistics, essentially), but for our purposes their differences are unimportant, and we choose to relate most of this type of data distribution with a smooth and continuous appearance.

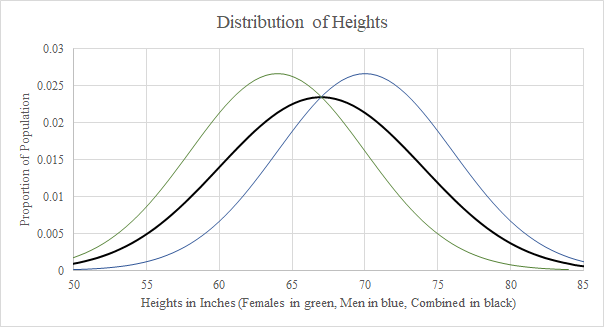
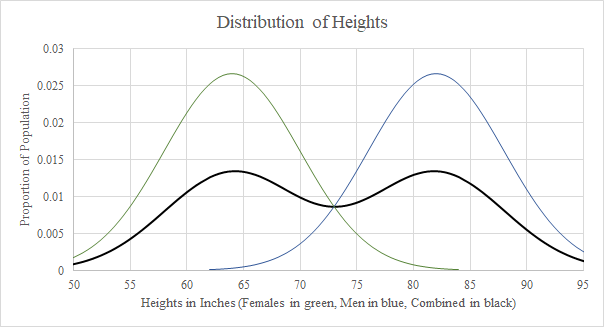
If you are unfamiliar with these statistical distributions, and you’re thinking, “But genes and other variables are not like coin flips. Some have larger effect sizes than others,” then you are both correct and thinking like a statistician! However, fast forwarding through a foundational statistics education, we note that most often the differences in effect sizes are not so large that a measured distribution isn’t approximately normal. For instance, even though the average height of U.S. men is six inches greater than the average height of U.S. women (sex as a significant variable makes around a 9% difference in height), the combined distribution of heights remains normal!

When the effect of a single variable is extremely large relative to all others, the resulting distribution becomes “bimodal”. For example, if we tripled the average difference between men’s and women’s heights by making all men a full foot taller, suddenly the combined distribution of men’s and women’s heights looks like a two-humped camel:

While many shapes are indeed possible, single-humped normal distributions are by far the most commonly observed in complex systems where no single input dominates.

---

The Value of a Weighted Coin

Suppose that you're a salesperson of some kind of luxury good like gold watches or fake vaccine cards. A potential customer strolling around your shop wanders in, and you engage in conversation. You show the potential buyer your wares as you educate them on the fine points of watch hands or saline solutions…

The best salespeople (defined by those who sell the most products) are those who understand their customers and their potential customers (and everyone else as a category, too, though the sales staff might not spend much energy on them when they can distinguish them by sight).

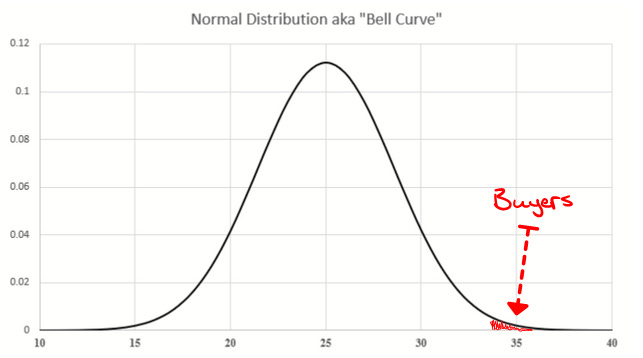
The seller of luxury goods knows that they're looking for that upper tail of the economic distribution. The best salespeople then find a way to nudge the curve. Like weighting a coin…just a little. It's easier to get 33 heads from 50 flips if the probability of flipping a head is 52% instead of 50%. Maybe by stroking the potential buyer's ego, or upselling the value of the status symbol…

How much higher?

That little nudge of the weighted coin more than doubles sales from 0.77% buyers to 1.61% buyers among the population (I'm using 33 out of 50 heads as the sales point). The salesperson who pulls that off dramatically increases his average payday.

---

Experimental Behavioral Economics

In 2010 the Behavioral Insights Team (BIT) was founded within the UK government as something like a small intelligence agency. Within a few years, the agency/team/firm/whatever was employed by governments, banks, media corporations, and education groups all over the world. And their affiliates include—who else? Sunstein and Thaler. Among other technocratic influencers.

In late January it was revealed that BIT was involved in COVID-19 pandemic messaging aimed at influencing the public.

What for and Why?

Some details are still unclear, but it appears that BIT directed media, government officials, and perhaps other trusted information outlets to instill fear and shame in the population of the UK in order to impose the public policies that somebody wanted imposed.

Who Would Want That?

That investigation needs to take place, but I'd start with FOIA requests of government documents, and move toward the vaccine manufacturers for questioning. There may be numerous forces at play. A great deal of wealth and power is at stake.

---

Mass Deformation

A couple of weeks ago I caught another discussion of Dr. Mattias Desmet's theory of Mass Formation Psychosis. I personally don't bother settling on a single specific theory of how social control is accomplished, but I'm extremely glad to see the conversation taking place.

I'd like to mention that I'd never watched Tommy's Podcast (TPC) before this airing. And while I'm generally wary of people who podcast with a background that is one overt display of jingoism, Tommy struck me as one of the most intelligent interviewers I've seen or heard in the podcasting world. I interpret him as "values first, flag second," which is the correct ordering of priorities, IMHO. I can see why he wound up being a point of convergence for several brilliant and busy minds. I've caught several of his interviewers since, and he has quickly moved into my short list of favorite podcasters. 

Without going too deep, I'd like to end (for now) on a thought worth chewing on. Social control has been around for a very long time. Some of it clearly starts within our educational system, and the media's role is to continually provide an authoritative presence. There is and has long been a whole lot of nudging going on in those information spaces. But consider for a moment the possibility that ratcheting the nudge game up a notch or two or ten or however many that technocrats can assault our minds with given the powerful machine learning algorithms at their disposal…consider that there is "too much to take" for each individual.

For how many people is that line being crossed?

Is society being…nudged over a cliff?