A Statistics Lesson: Understanding False Positives and Fear

The Chloroquine Wars Part XVIII

A recent article at Lockdown Skeptics claims that there are more false positives than true positives in recent SARS-CoV-2 testing of school children (please don't say "COVID testing" since COVID-19 is determined by symptom diagnostics, not PCR, antibody, or antigen testing). From the article:

Professor Jon Deeks, a biostatistician from the University of Birmingham, said in March: “We would expect far more false positives than true positives amongst those testing positive in schools.”

Some may wonder how this is possible given tests with high sensitivity and specificity. I'd like to take the time to explain using a piece of curriculum I wrote for my own students over a decade ago. First, I set the problem up with a story. Note that Professor Sergey Sarkisov was one of the teachers I employed at one of the schools I built and ran a number of years ago (the Mathematics, Informatics, Science, and Technology or MIST Academy).

After the students read the problem and context, we discuss what it would be to walk around untreated, with a "baby" toe bouncing (THU-THUD-THU-THUD) like a basketball. Next---and before walking through the problem of finding the probability that somebody who tested positive indeed has Sarkisov Syndrome (SS)---I ask students to write down their first guesses in their first seconds of thinking about the problem and hand them to me. I then read them out. Most all of them tend to be between 90% and 100%. Even those who guess lower are usually nowhere near the correct answer. In fact, I've even asked this problem in groups that include scientists, computer scientists, and math professionals and heard mostly answers that were not close to the correct one.

Experienced data handlers and statisticians who know how to apply Bayes' Theorem can work the problem out in a few seconds. However, we begin with a breakdown of all the categories of testing results.

From here, we compute the correct percentage:

Finding out that only 2 out of 7 positive results are true positives (and 5 of 7 are false positives) from such an accurate test (under an ordinary set of circumstances) often surprises people not steeped in well-earned statistical intuition. And in fact, the answer could be lower---sometimes far lower! If true positives are rare enough, even a test with 99% sensitivity and specificity both could yield less than 1 true positive for every 999 false positives (0.1%). In fact, zero percent is the lower bound among possible answers, and that depends on the proportion of infected residents. If nobody is infected, all positive test results are necessarily false positives.

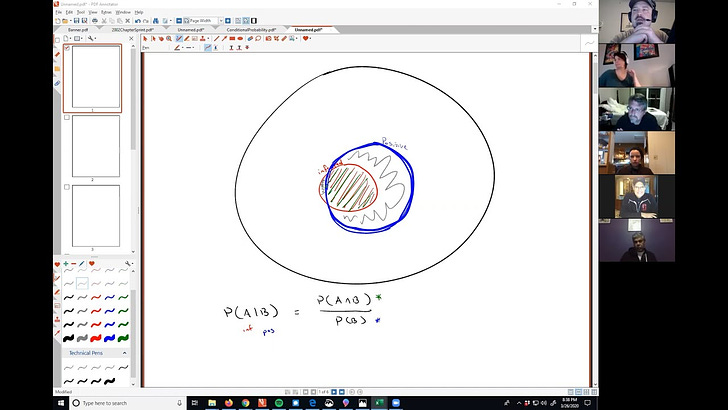
If you haven't watched the video above, this picture (grabbed as well as possible from the video) can help resolve any intuitive gap you might have:

The population is in the large (black) circle, but the total population of the city of Madison becomes irrelevant the moment we declare a positive test took place. That "conditional" statement of a positive test result means that we are now only examining the part of the population of Madison that tested positive---those in the blue circle. The probability that we are looking for is the portion of that population that is also in the red circle (the infected population) that partially intersects the blue circle. Now our logic reduces to understanding Venn diagrams and proportions of (population) sizes (discrete, but almost like areas in circles if we draw them well enough, which I don't).

What does this all mean?

Well, it's just a lesson. But perhaps the moral of the story is that a bunch of positive tests means nothing without further context. During this pandemic, a lot of information has looked far scarier than it really is. Sometimes it almost seems like the media seeks to induce panic---either for greater audience retention or possibly to gain social control on behalf of those who really pay their salaries.