Games of Trust
Game Theory, Part 3
"I wanted to explain that trusting is harder than being trusted." -Simon Van Booy
A word of encouragement: don't worry if you get lost in the technical jargon at first. Sometimes that jargon sinks in after getting your hands a little dirty, and that opportunity is provided below.
There is no one perfect model for human relationships. However, game theory at least models some basic economics of trust in terms of utility garnered from various decisions. These models come in two forms: normal form games and extensive form games. In this article, I plan to discuss a particularly challenging normal form game circumstance known as the prisoner's dilemma (see here, here, and here). An enormous portion of the world's problems—particularly the most challenging economic and political problems—are essentially prisoner's dilemma (PD) problems, or have versions of the problem embedded in them.
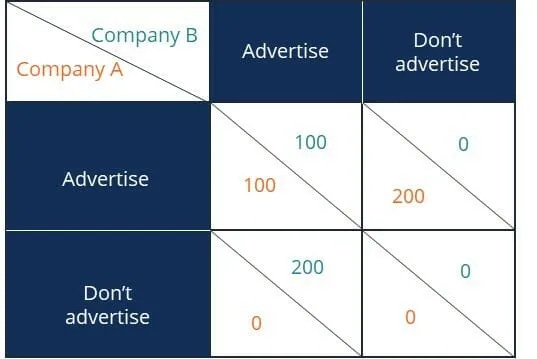
At some point in the future, I plan to write my own basic prisoner's dilemma article, for I'll let the links and video above suffice for now. The prisoner's dilemma is unique among basic normal form games because each player's rational decision is to defect, which has a lower overall "payout" than if each player cooperates. In technical terms, we say that the Nash equilibrium is for all players to defect. (Edit: for clarity, think of the example below in terms of a system in which everyone needs the service provided by Company’s A and B, so each customer converted comes from the other company’s existing customer base.)
Iterated Games are Different
While the prisoner's dilemma seems like bleak frustration, the game changes when participants repeat the game. We call such a series of games iterated prisoner's dilemmas (iPD's). In such games, it can be best to cooperate in order to maximize individual utility. Since judgment of "personality" comes into play, rationality takes a backseat to pattern recognition and pattern projection.
A few years ago, Nicky Case built a brilliant game that demonstrates the point in a relatively simple way. I encourage readers to play the game through, and then to consider the commentary about the various personalities they play against.
If you're game, you might then watch this video about Professor Robert Axelrod's strategic tournaments that used an iPD format.
There is still debate about "best strategies" in Axelrod tournaments, but it is clear that responsive strategies that are not doormats (always cooperative even against players who defect aggressively) or overly aggressive (defecting often to try to achieve short term advantages that might or might not be held long term) achieve better results (though the selfish, overly aggressive strategies dominate the passive doormats).
While this much study of PDs and iPDs is certainly quite educational, there is an interesting question of how best strategies change when the Axelrod tournament structure changes. What happens if the payouts change to make risks of cooperation more or less shallow? What happens when all players observe all games versus when only players see their own games? What happens when the payout structure changes, or the lengths of the game vary (possibly at random)?
These are among problems I've studied for a number of years, and at some point I'll write more about them—or perhaps team up with a computer scientist to study. I believe that the answers these variations of Axelrod's tournament produces will absolutely result in better models for economic and political decision making.
Final Question
What happens in iPDs in which participants are told that "winning" the most binary games (rather than total points accumulated, or vice versa) might result in immortality?
Is that what the plandemonium is about—at least to some degree?
Thanks, Mathew. The Nicky Case vid made my head spin a bit, but fascinating that different numbers of iterations using essentially the same variables produce different outcomes (if I got it right). Truth is stranger than fiction.
There is a point past which Game Theory just gets unweildy, though: once uncertainty about [epistemic, quantitiative, and doxastic] typespaces is introduced, the nut becomes uncrackable because there's no closed-form solution and no equilibrium.
Let's say that I _believe_ that my adversary _believes_ that our game has a specific payoff structure P, although my reading of the available information indicates that the actual payoff structure is P† with probability distribution ~A†(φ†) where φ† is a vector of parameters that characterise the (arbitrary) distribution A†.
My adversary _believes_ that I _believe_ that we're facing some other payoff structure P*≠ P†, with a different distribution (A*) characterised by different parameters φ*.
My adversary states quite openly that he uses haruspicy and astrology as his key methods. The latter requires him to know my birthday - which I _believe_ he can not possibly know. I also _believe_ that it wouldn't matter if he guessed my birthday correctly - given what I know about the usefulness of the set {haruspicy, astrology}.
Then I find out that his guess at my astrological sign is correct... 1 in 12 can be dumb luck (and has a 'tilt' if he guesses that I was born in the Upper Hemisphere - i.e., New Zealand[1]).
Does my belief about the usefulness of his method change?
One thing is clear: in multiplayer, multiperiod games with uncertainty, the 'rational' equilibrium will NOT HAPPEN unless
▪️ ALL of the participant behave 'rationally', AND
▪️ ALL of the participants believe that EVERY OTHER agent behaves 'rationally'.
The Stanford Encyclopaedia of Philosophy page on the Epistemic Foundations of Game Theory is interesting, especially the discussion of the paradoxes that arise from self-reference -> https://plato.stanford.edu/entries/epistemic-game/#ParSelRefGamMod
This is why Uncertainty Quantification is of paramount importance in all quantitiave endeavours, but has the (demotivating) paradoxical by-product that if properly implemented the outcomes of any realistic model have forecast bounds that look like an ear trumpet, and 'zero effect' is almost always in every useful confidence interval.
[1] New Zealand is a meme: it's not a real place. It was made up by Tongans and Samoans to prevent their islands from being over-run by Yanks seeking to escape world events. Their hope is that all the Yanks would head out into the ocean off Australia looking for this 'New Zealand' place, and would run out of food and water, and die.
They even invented a pretend-version of Polynesian (Maori) who aren't fond of Tongans and Samoans.
Crafty swine, those Coconuts.