Excess Death in the U.S. and The Lack of Mean Reversion

The Vaccine Wars, Part 65

Other Vaccine Wars articles can be found here. The RTE Locals community is here.

Early on during the plandemonium, I appreciated a lot of Dr. Roger Seheult's videos at Med Cram. He even included an early video on hydroxychloroquine, which YouTube censored during the propaganda campaign against the drug.

Since then, Dr. Seheult has been a striking example as to how overconfident a large portion of the medical community is of statistics. In some simple ways, physicians are better schooled than the average person. However, these are also individuals who received good grades in school—a stream of pats on the head that left many of them with a narcissistic shell that belies their relative understanding of the complexities of statistical thinking. Even worse than that, the physicians are then surrounded for their entire careers by biostatisticians, which is the most industry-motivated group of all statisticians, and which the larger statistical community has often and vigorously tried to disown (up until very recently when much of the Statistics community and the Mathematical Association of America gradually lost their spines, went woke, and largely stopped vocalizing any sense of conscience about the abuse of statistics in medicine in particular).

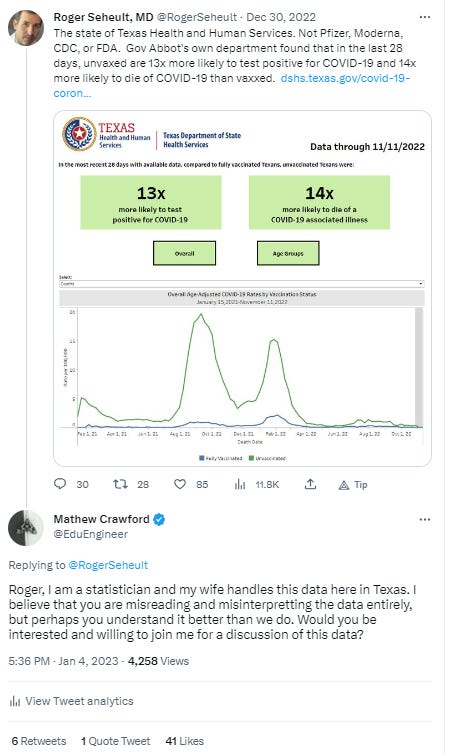
Here is one such example of Dr. Seheult projecting a dangerously incomplete sentiment:

Roger Seheult, MD @RogerSeheult

What's happening to excess mortality in the US by age group: As the beginning of November its essentially zero in every category except 75-84. But even that is dropping.

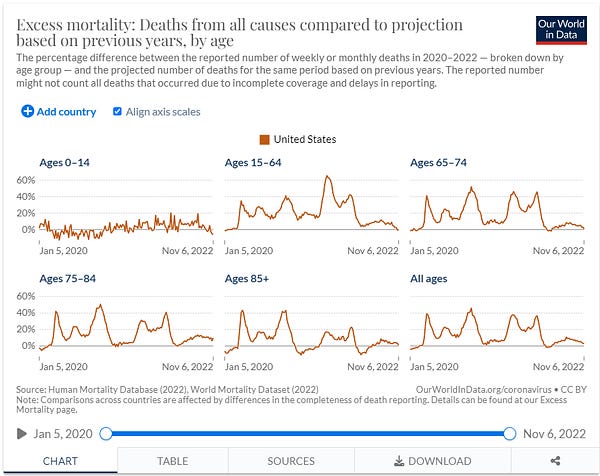
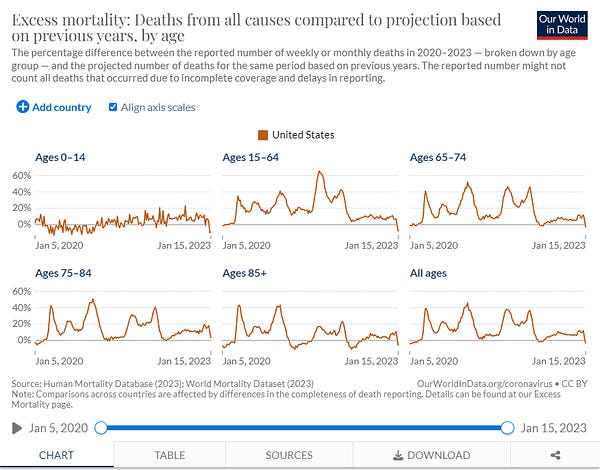
According to Dr. Seheult, there is now zero or near-zero excess mortality in the different U.S. age bands, and that's the end of the story. A few days ago, he echoed the point:

Roger Seheult, MD @RogerSeheult

Update: Pretty much the same:

But zero excess deaths is not the end of the story. In order to understand why it is not, we need to understand the definition of "excess mortality", and think through its usual patterns.

---

The Standard Mean Reversion of Excess Deaths

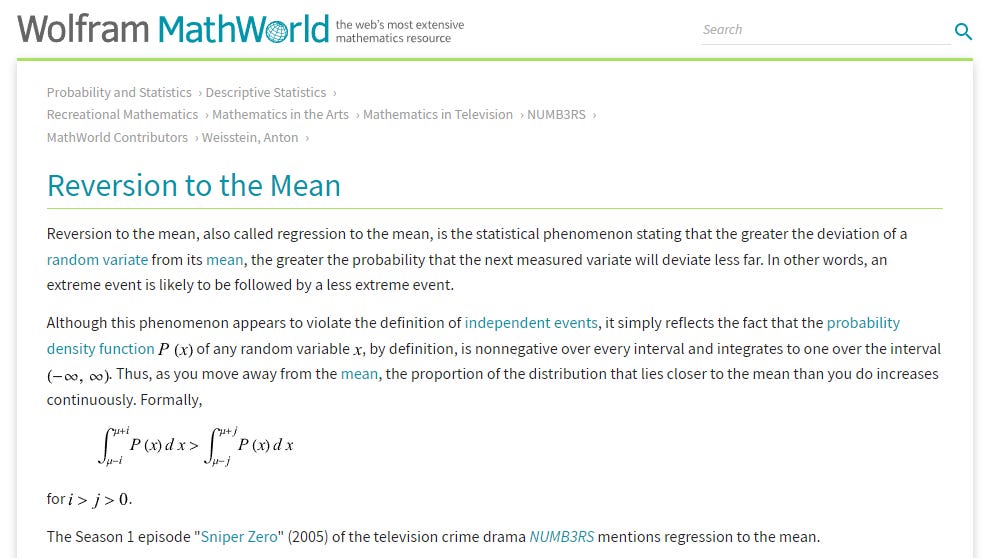
MathWorld describes mean reversion (also "reversion to the mean" or "mean regression") as, "the statistical phenomenon stating that the greater the deviation of a random variate from its mean, the greater the probability that the next measured variate will deviate less far. In other words, an extreme event is likely to be followed by a less extreme event." This definition is somewhat flawed or incomplete, but I'll ignore the subtleties for the moment.

Mean reversion is a statistical concept most often associated with finance where there are variable relationships that tend back toward a mean from which they deviate. While it is not necessarily the case that interest rates on 5-year and 10-year bonds mean revert, the lack of mean reversion would require a historically continuous and monotonic change in interest rates. Thus, people like me who (used to) trade bonds tend to expect mean reversion in the interest rate spread between bonds of different duration, by the same institutional issuer. Such expectations lead to a lot of trading opportunities.

Here is a simple example from Wikipedia that begins to get closer to a simple connection to present-day mortality circumstances:

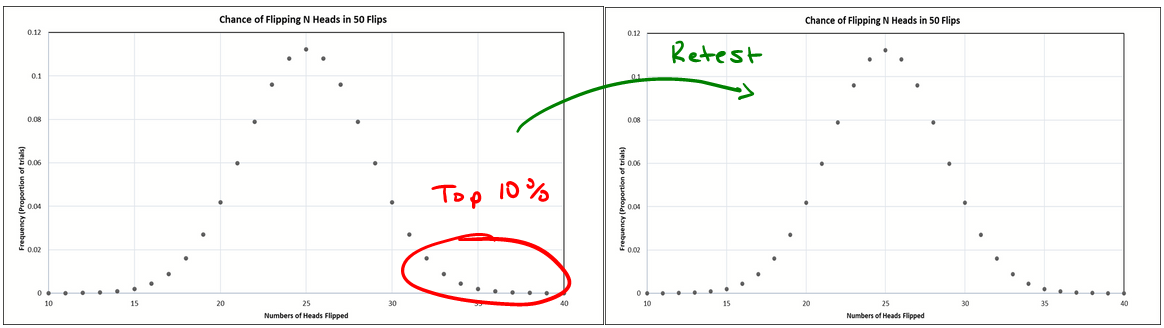
Consider a class of students taking a 100-item true/false test on a subject. Suppose that all students choose randomly on all questions. Then, each student's score would be a realization of one of a set of independent and identically distributed random variables, with an expected mean of 50. Naturally, some students will score substantially above 50 and some substantially below 50 just by chance. If one selects only the top scoring 10% of the students and gives them a second test on which they again choose randomly on all items, the mean score would again be expected to be close to 50. Thus the mean of these students would "regress" all the way back to the mean of all students who took the original test. No matter what a student scores on the original test, the best prediction of their score on the second test is 50.

We can only understand mean reversion on a case-by-case basis. The mean reversion of the bond yield spread takes place for different reasons than the simpler example. In the simpler example, the first set of scores includes only (conditionally) the top 10% of a random binary distribution of scores, while the second example to which it gets compared is once again random, so scores are expected to hover as a binary distribution around 50%.

---

Mean Reversion of Cumulative Excess Mortality

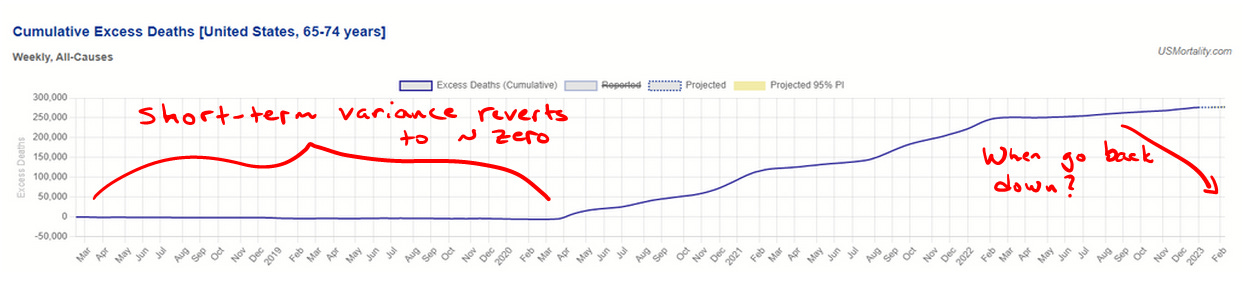
It is easier to see what (should) go on with mortality by looking at cumulative mortality numbers. Thankfully, Ben over at U.S. Mortality has nice charts for our purpose.

As we can easily see, cumulative excess mortality prior to the announcement of a pandemic tended toward zero (slightly less due to the fact that today's elderly are healthier than yesterday's elderly, in general). Any time those with weaker health profiles died in larger numbers, the remaining population of people with weaker health profiles shrank, so there was less potential mortality for subsequent periods until reversion was complete. From a zoomed out view, cumulative excess mortality is an extremely flat statistic—and for good reason. That Dr. Seheult repeatedly posts spot statistic excess mortality charts without discussion of this point suggests that he has no real sense for the meaning of the data. After a prolonged period of mortality associated with weaker health profiles, we should see a roughly equal period of negative excess mortality—unless there is an additional variable carrying healthy people into the weakened health profile. At that point, a neutral and concerned mind should absolutely ask, "Is it possible that the vaccines are that variable?"

As if we don't have enough reasons to ask that question, already.

---

A Familiar Pattern

Late last year, I tried to pull Dr. Seheult into a discussion about what I felt certain was his overconfidence in understanding statistics associated with vaccine effectiveness.

I wasn't the only stacker trying to bring him into a conversation, or explain his misunderstanding.

The Famous Medical Doctor and the Unknown Twitterer

Dr. Seheult said he was "all ears", but this is where communication gets difficult.

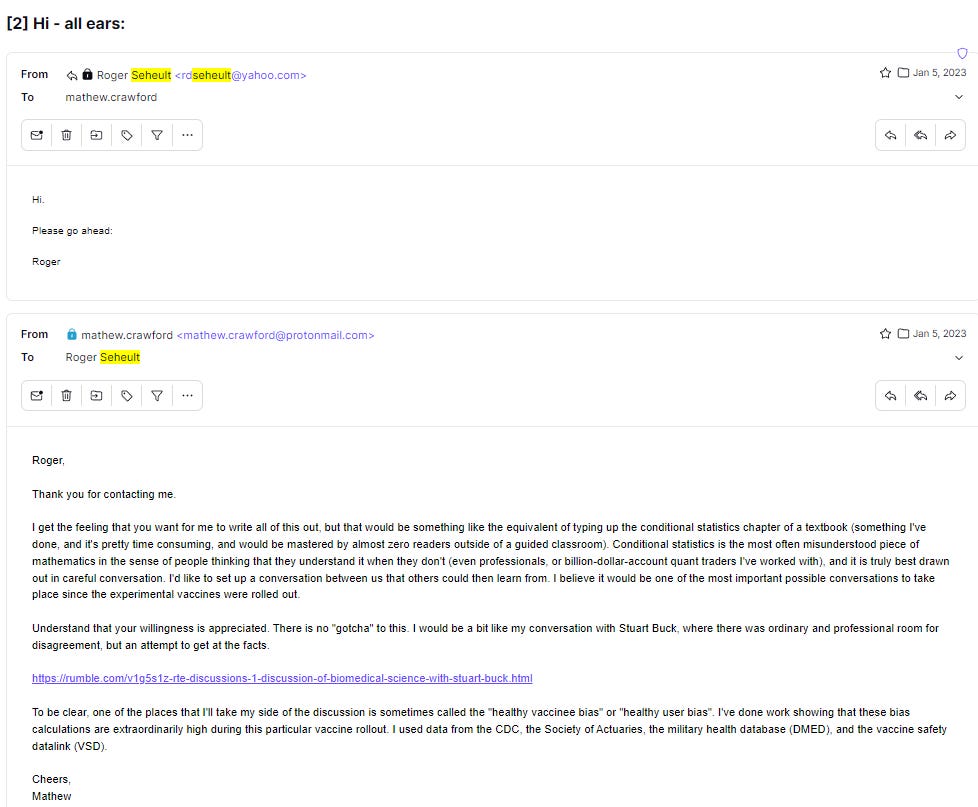
He did email me:

I feel like I can objectively say that I'm a pretty good math educator. Education is my first passion, though I've had a pretty wide career applying it to actuarial data, quantitative finance, materials engineering, machine learning, and the Human Genome Project, and elsewhere. Thousands of my students have gone on to the handful of top math, science, and technical universities around the world. They have collectively won scores of gold medals at the math and science Olympiads. They work at the highest levels of applied mathematics at places like Google, top hedge funds, and an array of pure and applied math disciplines in and out of academia. And yet, very few of them could have taught what Dr. Seheult needs to learn from an email exchange. And that exchange would have required perhaps 50-200 hours of writing on my part. Some of that is what is still ongoing in my Efficacy Illusions article series. For the most part, the good math students wind up that way because they submit to a reasonable give-and-take communication process. I spent more than 50 hours, for instance, working with my wife while she mastered graduate level statistics in her PhD program (she is now a bioinformatics instructor at a research university). These things take time, but Dr. Seheult wasn't interested in even one conversation that would likely have at least led him to confront some reasons behind his overconfidence.

Ultimately, I made this video without him.

He never responded. And that, in a nutshell, is a lot of what is currently wrong with the quantitative narcissism embedded in biomedical research. There are other factors, but this statistical miseducation, along with (and supporting) the charade of faux-statistical paradigms, are wrapped up in all corners of it. And that's where we are, folks.