"Democracy is based upon the conviction that there are extraordinary possibilities in ordinary people." -Harry Emerson Fosdick
And I believe that [that there are extraordinary possibilities in ordinary people]. I believe that confederations and democracies of power are important for other reasons, some of which are simply game theoretic in nature. I also believe that equilibria break and that challenges the human spirit and species to rise to a higher form. We can't just wish for goodness the same way we cannot wish for bandits not to ride down from the hills and take the crops. We must repeatedly address the incentive structures, and our investment in the framework is a misunderstood technology.
The other day, the 2000 Mules documentary came out (no, I haven't watched it, yet) and there is renewed interest in examining election fraud. I honestly do not know whether or not I'm the first to make all the observations I present here, but after a few dozen conversations with mathematicians, I think that some of my techniques are original. I was working on a paper prior to being sucked into vaccine statistics work. Really, I don't care whether this gets "published" beyond this substack. I just want to get the idea out there so that somebody (anybody) can make use of it.
Apologies in advance for the quick write-up. I have far too much to do to make this thorough and complete.
A Statistical Warning
"Absolute certainty is a privilege of uneducated minds-and fanatics. It is, for scientific folk, an unattainable ideal." -Cassius J. Keyser
Context is everything.
Before I go any further, I want to make this statement about statistics: there is no such thing as a correct or incorrect "method" in statistics—there is only the judgment of an observer as to how meaningfully the results match reality. I say this in order to pre-empt all conversation about whether or not Benfor's law (BL) "can" be applied to election results. There are (at least) two crappy arguments.
BL always provides a test for the sanctity of election results. (Technically false, though it often provides us with interesting observations and starting points.)
BL cannot be used as a test for the sanctity of election results. (Sort of technically true, but only in a vacuous sense that is horrifically misleading.)
Always look at statistical results with respect to the big picture. Always. Numbers don't mean anything in a vacuum. Of course statistical tests can be applied. And they certainly narrow down interesting localities for investigation. But any good investigation involves further examination of the facts. Context is everything.
Benford's Law
"Most people use statistics like a drunk man uses a lamppost; more for support than illumination." -Andrew Lang
Benford's law became famous (or "famous" relative to what can possibly happen with clever mathematical tricks) in the aftermath of the 2020 U.S. election. Numerous investigators noted observations of voting patterns that seemed to defy expectations.
First, let's talk about what BL says, and why. According to Wikipedia,
Benford's law, also known as the Newcomb–Benford law, the law of anomalous numbers, or the first-digit law, is an observation that in many real-life sets of numerical data, the leading digit is likely to be small.[1] In sets that obey the law, the number 1 appears as the leading significant digit about 30 % of the time, while 9 appears as the leading significant digit less than 5 % of the time. If the digits were distributed uniformly, they would each occur about 11.1 % of the time.[2] Benford's law also makes predictions about the distribution of second digits, third digits, digit combinations, and so on.
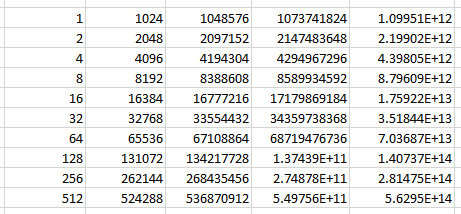
The unsophisticated version of BL is that in distributions that have a particular property called scale invariance (okay, that's not entirely unsophisticated), we see a non-uniform pattern among the leftmost digits of the numerals that represent the data. This isn't really surprising to a statistician, but it can be befuddling to nearly everyone upon a first encounter. Here is an example: exactly 15 out of 50 consecutive powers of 2 have a leftmost digit of 1:
1, 16, 128, 1024, 16384, 131072, 1048576,...
In fact, this is true for almost any 50 consecutive powers of 2, though once in a long while, there will be 16 with the leftmost digit of 1 instead of 15. In this exponential distribution (exponential distributions are nearly always the kind to which we apply BL), we can begin to form an intuition as to why BL works: A power of 2 is [approximately] 0.301 powers of 10.
Or, written differently, the base 10 logarithm (the "anti-exponential" given the inverse function relationship) is
There are tons of distributions to which BL applies precisely because there are tons of exponential distributions. The two most common examples are populations and money. These do not even have to be growing exponentially at any one particular moment to conform relatively well to BL! The 26% of American states with populations that have a leftmost digit of 1 is fairly typical of such data sets, though 30.1% would be the expectation.
The nice thing about Benford's law is that it doesn't take somebody with a PhD to apply. Here are some BL results run by one of my college debate partners (who is more quantitative than 95% or more of college graduates, and uses data in his work, but has not done the work of a theoretician).
Benford's Law and Election Results
Here is where things get controversial. There were some anomalous BL signals during the 2020 election. These signals were met with overly simplistic arguments from both sides (and a tiny few really good arguments). I have pre-empted these, so we can proceed in a sane manner.
Before we go very far, I want to point out this 2018 blog post about 2016 election results in which counties in Wisconsin that conformed poorly to BL just happened to be those that used Dominion voting machines.
This is already enough to establish context (meaning for further investigation), though this context may or may not extend to all circumstances. Here is a github repository of BL test results that I saved during the election controversy. There is discussion here about the results. Some of these show Biden voting not conforming to BL very well. For example:
But the arguments begin here with observations that the sizes of districts throw off these distributions. And they do! In particular, they should throw off the majority vote the most. For instance, if each voting district has between 400 and 1,200 residents, then there is not a full range (order of magnitude) of population. If the result were the most serious kind of landslide, we would not even see 2 or 3 as leftmost digits, and we would not see 1 often enough.
So, do we just give up applying BL in these situations?
Not if we are clever, and that gets us to the point of this story…
Widening the Application of Benford's Law: Other Number Bases
There are actually a whole bunch of ways to make Benford's law a more incisive tool for forensics work. One simple one is to test the leftmost digit rule of a set of numbers after converting them to another number base, like 8, 9, 11, or 12. There may be cases in which the criminals know just enough statistics to fake the base 10 distribution, but not enough to generate their dataset as an exponential distribution plus randomness [of some kind], which is what would be required for Benford's law to be thwarted when numbers get numerically expressed in any ordinary base number system.
The "leftmost digit(s)" stats are a little different, however. For instance, while 30.1% of population data should begin with (leftmost digit) a 1 when expressed in base 10, we should expect for that proportion to be 31.5% when the same numbers are expressed in base 9.
That's cool and all, but we can go further…
Widening the Application of Benford's Law: Funny Number Bases
Here is where we get freaky with Benford's law. Ready?
There is nothing about BL that requires it to be applied to numbers expressed in base 10. In fact, we don't even need to use an integer base! We can use fractional bases, and even bases less than 2, which allows for us to examine the results in districts of constrained size. I know that this is where I lose the general reader, but the mathematicians/statisticians reading here will get it. Here is a paper that I was writing up over a year ago, but quit because duty called with respect to vaccine research:
(Oops, much of the paper disappeared in the newsletter. Fixing now…)
I think I have to type words before the sections to get them all to show up…
Typing more words…
Some day in the future I hope to come back to this work and finish the paper I started.
Sorry for the typos and unfinished nature of the paper. I believe that this is enough for the smart people working on election results to understand the BL filter. Some people apply BL to one or two digits only, but this filter may require examination of a dozen or more digits. But that's not really a big deal to a good programmer.
Have fun with it. And if you know somebody doing statistical work on election results, please forward this.






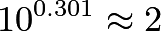
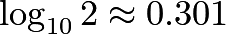

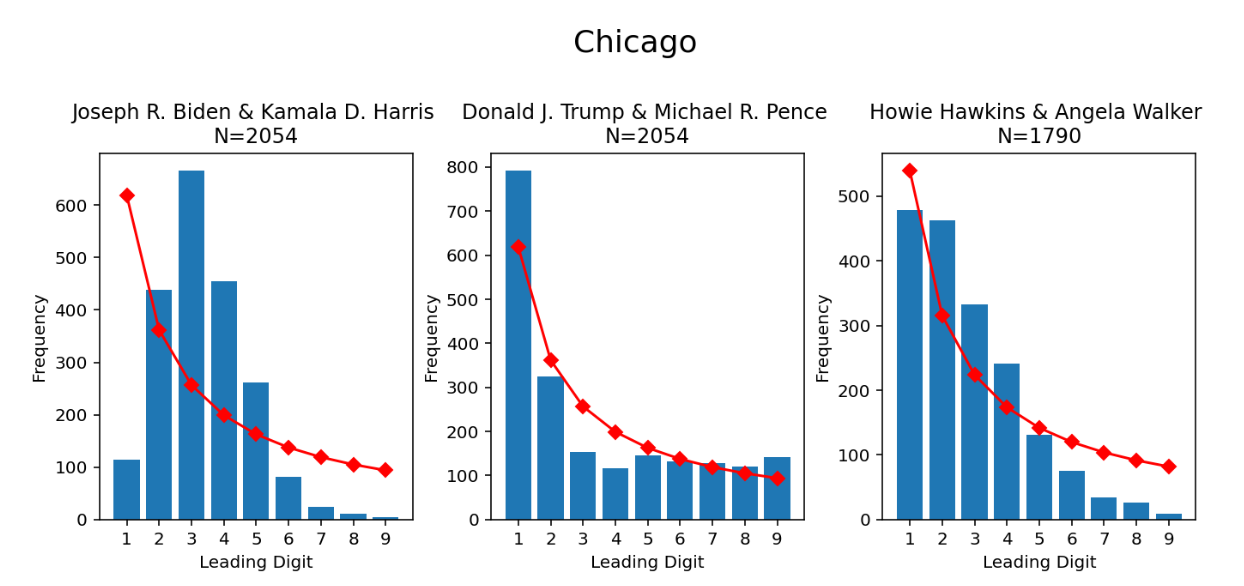




I was reading Benford breakdowns the day after. They stole that fuckin election.
Excellent job widening the use of the tool! Let’s call it Extended (or Generalized) BL.
One thing that drives me crazy is people equivocating voter fraud and election fraud. I understand that all the talking heads do, which doesn’t help. And even historical uses appear to admit this thing I consider a mistake. Perhaps it’s intentional. As in, to cover the more pernicious issue.
I think it’s important to distinguish between front end fraud and back end fraud. The back end fraud being machine- and hand-counting for example, and the front end fraud being illegal voting and fake ballots for example. The illegal voting seems to be what the powers that be want us to argue about. But the data suggest it’s the lesser problem, and in most if not all cases doesn’t make a difference in outcomes. I’d like to see serious research conducted into each facet, starting with the most pernicious. Extended BL seems to be a great tool to illustrate geographic areas where the research is worthwhile.
Another thing that drives me crazy is the tribal nature of this issue. Red team didn’t seem to care too much when Trump seemed to benefit. Blue team seemed downright giddy when Biden benefitted. In fact, a blue team friend of mine has been railing against this kind of fraud since 2004. When I brought it up for 2020, his answer was something like, “well, our team finally got one, so I’ll become active again next time”. A red team friend of mine won’t entertain the idea of issues in 2016. Until and unless we approach this apolitically, we’re all doomed. I personally haven’t voted since 2000, after I became convinced that fraud has decided every election since. With more research, possibly all the way back to 1960. Real apolitical research will horrify the public and undermine the US on the global stage. That’s why I think it’ll never happen. Instead, we’ll be given the pressure release valve of voter ID and illegal voting as a distraction.
Lastly, 2000 mules is extremely distressing to me. Most people watching it that think there was fraud will be too wrapped up in the “proof” that they will miss the methodology. Pay close attention to the methodology (first 35 minutes ish). It shows that we’re a breath away from digital slavery/imprisonment. The group of people most likely to resist will be the same people paying attention to the “proof” not the methodology. They are then primed into thinking the methodology is ok. It isn’t, and we should all be horrified that people with enough money can buy this. We’ve created an industry that will help law enforcement bypass critical safeguards to keep them from abusing citizens. It’s not ok. Not even when it helps your cause. If it’s not ok for your enemy to use it against you, then it’s not ok to use it against your enemy.
And anyone using the, “well it’s gonna be used/done by them/someone, so why not me?” argument should know that’s how George Soros sleeps at night. Go find the video interview where he explains his role helping the nazis. I mean, I’m not perfect either - I might even have made the same decision as him at that age (13) - but I’m disgusted nonetheless that he doesn’t show regret or remorse. Even if I made the same decision, I doubt I’d say anything more than, “I’m sorry”. Reporter: “How do you sleep at night after helping the nazis?” Ideal Soros answer: “I don’t.”