A Mathematical Solution to the Tiny Homes Initiative
Appreciating Mathematical Beauty Volume II
In late January, I spent five days at a convention of parallel community builders (agorism, Game B, and however else you might describe it). I plan to write more about that another time. For now, I'd like to write about one of the excellent projects I discovered while there.
https://abundancebuildingconcepts.com/our-homes/
Update (June 7, 2022): Several commenters worry about the non-squareness of the home, but this new video shows that the interior is more completely usable space than one might imagine.
Call it a tiny home if you like, and it could certainly serve the same function, but it could also serve as a "simple home" for those who don't need the luxury of something larger. At 400 square feet and a projected cost of $10,000 (if I understood correctly from talking to the designers), it fits a lot of possibilities. Bury one of these domes in the side of a hill under a bit of sod (the concrete dome is tough) and maybe you have a root or wine cellar. Or a hobbit hole. Two or three together could form a larger structure where needed.
Here are my new friends Grant and Gustavo explaining the simplicity of the Catalan Vault:
You can find a number of similar and related architectural styles here, but I suspect this is the first, "unfold and just add water" version!
Perhaps the world suffers from a bit of ancient amnesia. Let's have a little fun exploring the discrete side of technological wonders, which likely gives historical insight into how some ancient architectural masterpieces were accomplished.
The Catalan Numbers
The following problems may not seem relevant to architecture, but as we will see, they…might be? Further, I suspect that great architects of centuries past knew more about practical physical mathematics than was recorded in history—knowledge possibly passed down through a small network of superior students to each master.
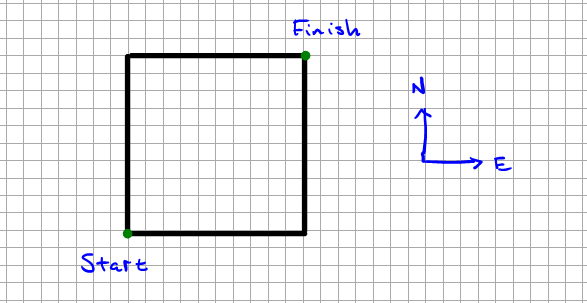
The first problem we are going to tackle is a path walking problem. If you ever took a course on or involving combinatorics, you probably remember these problems. If we count the number of paths that follow the gridlines from the lower-left to the upper-right, moving only up or right (north or east), then there are "20 choose 10" possible paths.
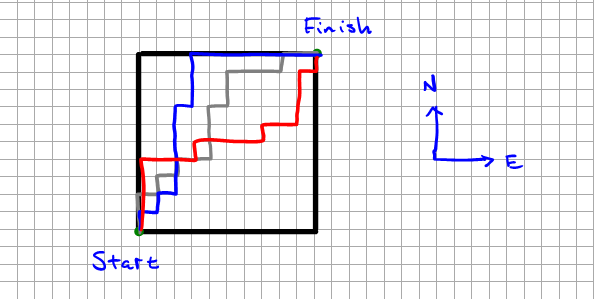
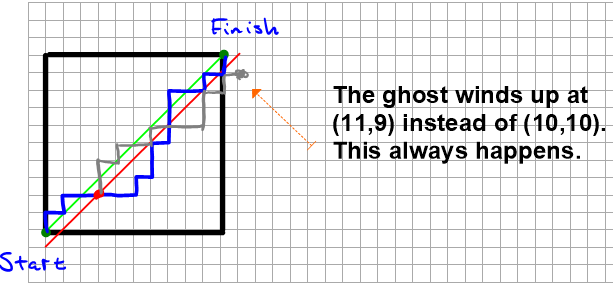
But we are going to tackle a more interesting and challenging problem. We want to count the paths that stay on or above the main diagonal. Perhaps examples are in order. In the following diagram, the silver and the blue paths satisfy the condition of never crossing below the main diagonal (always at least as many N moves as E moves from start to finish), while the red path fails (so it would not be part of our count).
Note, our problem of counting paths that stay on or above the main diagonal is equivalent to the following problems (and also many others):
Counting the number of syntactically correct sequences of 10 + 10 = 20 parentheses (for example, ((())(()(()))()()()) always has more open than closed parentheses from left to right).
Counting the number of ways to triangulate a convex dodecagon, which is to say chop it into only triangles whose vertices are vertices of the original polygon.
The Mountains of Catalan version.
It may be enjoyable for some readers to think through why these problems are equivalent if you never have before. These equivalent problems involve some nifty additional lessons of their own (perspective alters the ease of different approaches), but for the moment, we will focus on our path walking problem. Let us leap into the clever approach, and specifically my version of that approach.
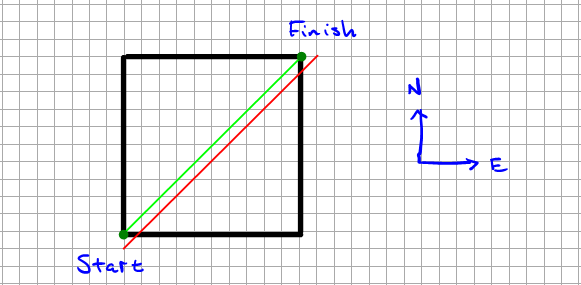
The goal of staying on or above the main diagonal (green) is equivalent to the goal of never touching the diagonal of doom (red). Make sure you see why or…DOOM!
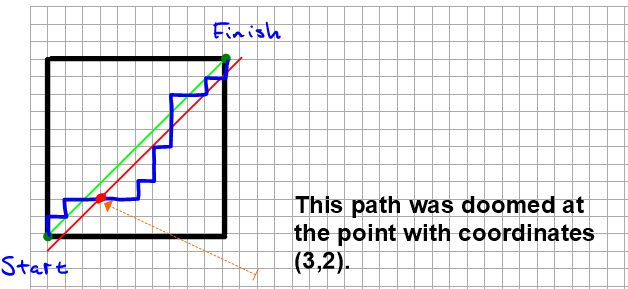
Many excellent solutions to counting problems involve focusing on what we don't want to count rather than what we do want to count (when that's easier). We call this complementary counting, and we apply it here. We will count the "doomed" paths that do touch the dreaded diagonal of doom, like this one (in blue):
Note that every point on the diagonal of doom has coordinates (m+1, m), where m is some integer appropriate to our range. The blue path above was doomed when it hit the point with coordinates (2+1, 2), or (3, 2).
Now we take advantage of symmetry. At the moment (point) of doom, let us imagine the body and soul of a person traversing the blue path to "split", with the ghostly soul thereafter walking a path that is the mirror image of the blue path reflected over the diagonal of doom (red line).
The ghost always winds up at (11,9) because,
The first leg of the path (first 5 steps in this case) to (11,9) is just the blue path to (3,2).
After that, the blue path must go North once more than East to reach (10,10) from (3,2), so the silver ghostly path does the opposite, going East once more than North.
So, the ghostly soul winds up two steps further East than North in total after the 20 total steps—once during each of the two path walking parts (up to the doom point, and thereafter).
What this means is that for each (blue) path that hits the diagonal of doom, there is one and only one path where the ghostly soul can "take over" and complete the walk, which necessarily finishes at (11,9). So, the number of such paths is 20C11. The remaining paths must therefore remain on or above the main diagonal (green), so there are
such paths. Or, more generally, for an n x n grid.
The first solution to this problem came from Spanish mathematician Eugene Charles Catalan (1814-1894). Hence, the numbers Cn are known as Catalan numbers. And if you're wondering if there is some exceptionally beautiful proof that just says that 1 out of n+1 of the random walks remain on or above the main diagonal…yeah, well me too! And if there are any exceptional mathematicians reading who know, this is one of those moments when I'd rather you not spoil it because I'd rather it remain a wonderful mystery to take a walk and think about once a year or so. But if this remains an unsolved problem, I'd be happy to have that sourced.
Back to Architecture
The Catalan numbers are the answer to a two-dimensional counting problem. How does that relate to a three-dimensional architectural structure?
I wasn't sure that I could answer that question when I started working on this article. I learned about Catalan numbers as a teenager, but was never as strong a geometer as I was with discrete math. I'd heard of Catalan solids, but wasn't sure if there was a relationship to the Catalan numbers. I am certainly no master architect, and I'm piecing together my latent understanding of the solid geometry on the fly, so forgive me if I make a mistake or two. I'm happy to learn from a greater geometer who may stumble along this post. But…crap, I was unable to unravel the complete connection in my hotel room in Austin, and I haven't really had free time to work on it since.
Oh well, let's see if we can establish some vague connections among Catalan's mathematical passions (assuming they're related, which they might not be at all).
The protrusions of these 13 solids are all regular pyramids, which are protrusions from the 13 Archimedean solids, with chirality intact for the snub cube and snub dodecahedron (which may excite some math/physics geeks). Regular pyramids are extremely strong structures. If we take the polygonal nets or quasi-nets (same tiling repeated as needed), and stretch them out without completing the folds into closed solids, we can achieve dome-like structures: geodesic domes.
This time lapse of the construction of a Catalan dome shows a key feature of the architecture: the triangular frame. Catalan domes can technically be built without the triangle, but the triangle is the "strongest" polygon. If somebody hits you in the face with the corner of a cardboard polygon, you'd rather have that polygon be of many sides so that it would "give" and fold in. That doesn't happen with a triangle.
Really, arches can be thought of as fractalized triangles. They do not buckle under pressure until the building material itself is somehow broken. The discrete approaches the continuous model, asymptotically according to the sizes of the tiles or bricks.
So, here's where I am now:
Catalan numbers are also counts of Catalan mountain ranges, which is like a fractal representation of a simple set of (strong) triangular structures.
Catalan numbers also count triangulations of polygons.
These are part of my lesson on Catalan numbers, and certainly have potential for direct relationship to Catalan domes and vaults. But is there any relationship?!
I Give Up
I finally broke down and searched the internet, finding this article on Catalan vaults at Wikipedia. It turns out that the architecture is more due to a different Spanish genius, Rafael Guastavino, but was later named after Catalan—very possibly due to the reasonably entertaining notion that the Mountains of Catalan and Catalan Solids must surely relate to the architecture. Maybe there is some wonderful discretization of these arches and domes that relates back to Catalan, but that is beyond my two hour skill level, and possibly far beyond.
And there I will retire. I hope you are as entertained as I am.
Historic American Engineering Record; Library of Congress HAER NY,31-NEYO,86-49





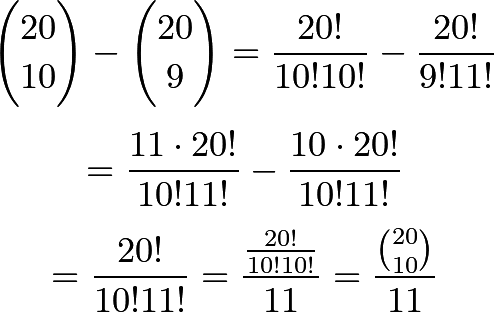
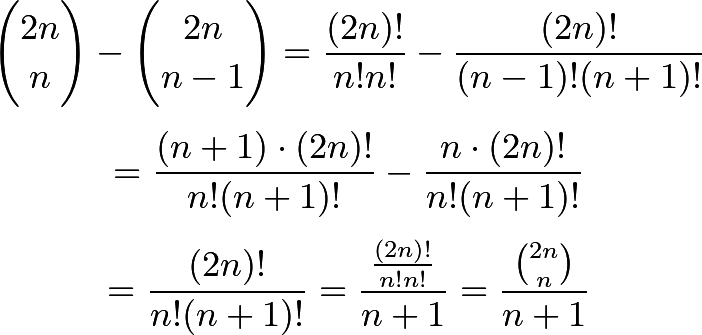




Matthew, super intruiging article you are a Grand Canyon of knowledge and interests. I do cad and drafting, (talk to me) and I want to live in that little space. If my house was closer to paid off, I would love to tear it down and make 2 of these on my lot, so the rest of it could be food. Living in these 100 year old hard to heat and cool houses is not easy and makes little sense when we need to grow our own food. Best
"Tiny homes", a.k.a. kennels. When Charles Schwab, Emmanuel Macron, Justin Trudeau, Barak Obama, Bill Gates, and Al Gore all move into one, I may start thinking about it.