A Cute Problem: Genetic Engineering of the Narrative
Appreciating Mathematical Beauty Volume I
I don't want for my substack to be about war all the time. It's just that during war time, the importance of war topics is thrust upon us.
The primary goal of Rounding the Earth is educational, and broadly. And I believe that an education that doesn't slow down to observe and absorb beauty is sadly lacking. So, I'd like to deliberately start slipping in articles about various forms of beauty. While some articles, like this one, might involve little mathematics gems, there will be no limits placed on the topics aside from my own experience.
Some of these articles may be behind paywalls assuming they do not relate to health, broadly.
The Cute Problem About an Acute Problem
At a later date, behind a paywall, I will give sources to original versions of problems such as this one, but I would rather not ruin the joy of the experience for those who delight in solving.
The problem is a little wordy, and that's part of CNN's goal. They don't really want you to understand the problem. Don't worry—you got this. Let's consider a valid series of statements of affirmation that can be made by a CNN member, just to be sure that we understand what's going on.
Consider the adventures of CNN member Sanitary Goopta and let n = 5. During the pandemic, Goopta makes the following declarations in order, opening with the obligatory,
"CNN is the appropriate arbiter of truth during the pandemic!" (PPE #1)
Then the statements of affirmation (all of which must be different in content):
"Poor people and children should wear masks!" (PPE #2)
I don't think that "Republicans should be permanently locked down," (PPE #3) but I do think that, "Everyone needs to be vaccinated before we have long term fertility data." (PPE #4)
"People who aren't vaccinated should not receive medical care!" (PPE #5)
Today I reject the notion that "CNN is the appropriate arbiter of truth during the pandemic!" (PPE #1), but "Poor people and children should wear masks!" (PPE #2)
"Republicans should be permanently locked down." (PPE #3)
"Everyone needs to be vaccinated before we have long term fertility data." (PPE #4)
I strongly disagree with "People who aren't vaccinated should not receive medical care!" (PPE #5), but affirm that "CNN is the appropriate arbiter of truth during the pandemic!" (PPE #1)
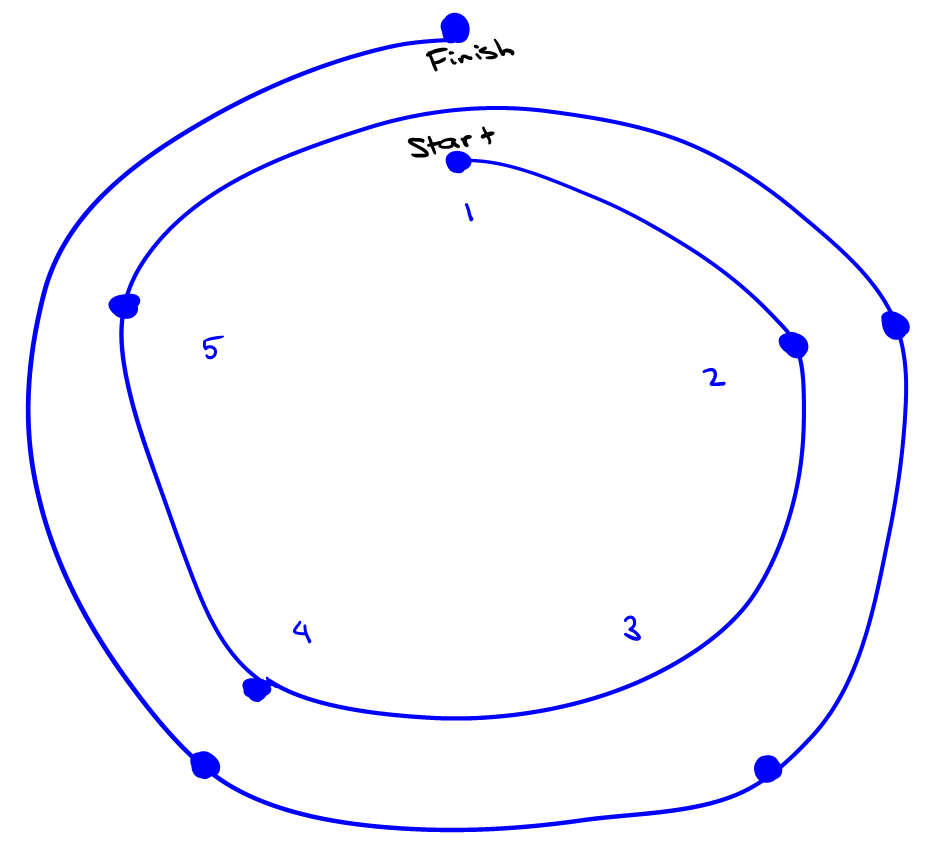
You might visualize this sequence as circular daily affirmations (blue dots spiraling outward). That helps get rid of all the wordy words. We can see the process come full circle and then repeat itself. That's how The Science works!
We can also ignore the blatant internal inconsistencies, and look for a way to simplify the sequence of statements:
1Y, 2Y, 3N, 4Y, 5Y, 1N, 2Y, 3Y, 4Y, 5N, 1Y
This simplified view of Goopta's daily affirmations might be easier for a lot of problem solvers to work with, but it's still a bit cluttered for my taste. Maybe we can use the circular image to guide even better codification of our example.
1Y, 2Y, 3N, 4Y, 5Y, 1N
1N, 2Y, 3Y, 4Y, 5N, 1Y
I went ahead and repeated the (1N) rejection of PPE #1 in order to line up the data in a 2 x 6 matrix. More generally, this would be a 2 x (n+1) matrix. And really, we can now leave out the numerals because they are implied by position:
Y, Y, N, Y, Y, N
N, Y, Y, Y, N, Y
We have now codified a CNN member's behavior with a simple binary matrix (represent the N's and Y's as 0's and 1's if you like).
You may now wish to read back through the example of Goopta's statements of affirmation to make sure you've followed along with our modeling process before moving forward. If you recognize the statements as encoded, you're halfway to a beautiful solution already.
En route to solving the given problem, we need to determine the maximum number of CNN members possible. We do this by counting the number of possible sequences of statements of affirmation that obey the Byzantine rule set. And now we can perform that feat by counting the number of possible matrices.
But wait! We can make use of genetics!
"Like that stuff that Eric Topol doesn't understand?"
Precisely!
Follow me on this one…
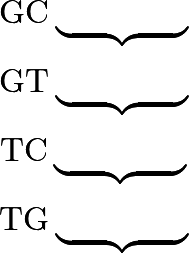
Every column is a pair of binary values, so there are at most four possible columns. Let us name them like genetic bases:
This allows for us to rewrite each possible matrix that we want to count as a simple string of letters!
What an excellent model for our counting problem! Now we just need to reframe the CNN restrictions on statements of affirmation in terms of these genetic strings, then find a way to count them up.
Note that since PPE #1 must be affirmed at the start and end of each sequence, that a 1 must appear in the upper-left and lower-right of each candidate matrix. Thus, each corresponding genetic string can only begin with a G or T, and can only end with a C or T.
Next, since a PPE rejection must always be followed by an affirmation in a statement of affirmation, two 0's can never appear consecutively. This prevents A's, C's, and G's from appearing consecutively. But T's cannot appear consecutively, either, without violating the rule that disallows repeating a statement of affirmation! (Try to think through why that is if you don't at first see it.)
Finally, we note that A's cannot appear at all. Each of the two 0's in a matrix column would necessarily be followed by 1's, representing a rejection-then-affirmation pair of a repeated statement of affirmation.
Now we are ready to solve the problem, and the task is quite simple from here. We are counting sequences of length n+1 of three letters C, G, and T, for which the only remaining restrictions are that we do not start with C, do not end with G, and we do not repeat consecutive letters.
We can do this constructively. There are 2 possible ways to start.
Then there are 2 possible ways to continue each string (since we cannot repeat a letter consecutively).
The number of legal strings keeps doubling for each letter that we add. For 6 letters (where n = 5), there will be 2 to the 6th power genetic strings. However, there is just one problem, which is that we cannot end a string with a G. So, some of our 2 to the power of 6 strings do not form valid sequences (of affirmations). Oh, misery, our plan seems ruined. RUINED!
Fear not. If we just snip any pesky G off the end of one of these invalid genetic strings of length 6, we get a valid genetic string of length 5 that necessarily meets all our restrictions without ending in G. What's better is that every single valid genetic string of length 5 (representing a sequence of statements of affirmation for n = 4) can be achieved in this way!
What we just demonstrated is that the number valid genetic strings of length 5 (the maximum number of uncloned CNN members who can differ in their daily affirmations of 4 PPEs) plus the number of valid genetic strings of length 6 (the maximum number of uncloned CNN members who can differ in their daily affirmations of 5 PPEs) sum to 2 to the 6th power, and the entire argument generalizes for any n that fits the problem. QED.
Readers without substantial experience with combinatorics may find the lack of computation involved in this problem surprising. Indeed. For much of mathematical domains of combinatorics, probability, and statistics, the modeling process is the vast majority of the effort. Therein lies the opportunity for beautiful work.
Hopefully, too, that helps readers understand why I do not focus on producing charts so much as I work on the logic connecting every important aspect of the world to each analysis. As I often say, when the calculations aren't connected to the real world, that's just computational masturbation. I'll leave that to the pharmastats folks.
Closing Thoughts
Some solvers, including professional mathematicians may enjoy this solution, but may also dismiss the genetic strings as artificial. After all, we certainly could have used any four (or just three) letters of the alphabet. That is true, but it also misses the opportunity to dive down the rabbit hole that is DNA computing.
But at that hole I'll step away with a, "I hope you enjoyed the presentation," and, "I was never really here."






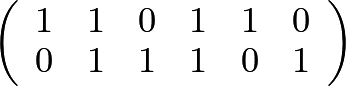
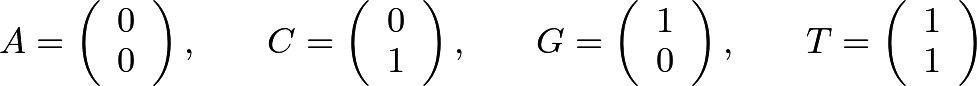
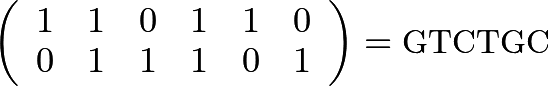


Okay. So what size n, if n = PPEs, does it take for CNN to achieve zero transmission of Truth?
Considering a layered mitigation strategy... which I hear works... the more layers the better... your PPE protects me, my PPE protects you...
Or can we only asymptotically approach TruthZero? Scary thought.
Can we achieve TruthZero? Or do we need to learn to live with Truth? What if there is a reservoir of Truth out there? What if Truth propagates through animal hosts who can't choose their pronouns? Perhaps Truth is already endemic.
Maths = racism and bigotry